Analogi är ett slags likhet. Liknande föremål överensstämmer med varandra i något avseende, analoga föremål överensstämmer i vissa relationer mellan respektive delar.
1. En rätvinklig parallellogram är analog med en rätvinklig parallellepiped. Relationerna mellan parallellogrammens sidor liknar nämligen relationerna mellan parallellepipedens ytor. Varje sida i parallellogrammen är parallell med bara en annan sida och den står vinkelrätt mot återstående sidor. Varje yta i parallellepipeden är parallell med bara en annan yta och den står vinkelrätt mot övriga ytor.
Låt oss kalla en sida ett "begränsningselement" i parallellogrammen och en yta ett "begränsningselement" i parallellepipeden. Vi kan då förena de båda föregående utsagorna i en enda som är tillämpbar på både parallellogrammen och parallellepipeden: Varje begränsningselement är parallellt med bara ett enda annat begränsningselement och står vinkelrätt mot övriga begränsningselement.
Vi har alltså uttryckt vissa relationer som är gemensamma för de två system vi jämförde, rektangelns sidor och parallellepipedens ytor. Analogin i dessa system består i att de har gemensamma relationer.
2. Analogier finns med i allt vårt tänkande, i vårt vardagsspråk, när vi drar våra enklaste slutsatser, lika väl som i konstnärliga uttryck och vetenskapliga resultat. Analogier används med olika precision. Ofta används vaga, tvetydiga, ofullständiga eller ofullständigt klargjorda analogier, men analogier kan också nå en nivå av matematisk precision. Eftersom alla slags analogier kan spela en roll för upptäckten av lösningen till ett problem bör vi inte förbise eller ringakta något slag av analogi.
3. Vi kan skatta oss lyckliga om vi, när vi försöker lösa ett problem, lyckas upptäcka ett enklare analogt problem. I avsnitt 15 handlade vårt ursprungliga problem om diagonalen i en rektangulär parallellepiped. Genom att studera ett enklare analogt problem, som handlar om diagonalen i en rektangel, fann vi lösningen till vårt ursprungliga problem. Vi skall diskutera ytterligare ett fall av samma slag då vi löser följande problem: Sök tyngdpunkten i en homogen tetraeder.
Utan kännedom om integralkalkyl och med endast små kunskaper i fysik är detta inte alls något lätt problem. Det var ett stort vetenskapligt problem på Arkimedes eller Galileis dagar. Om vi alltså vill lösa det med så litet kunskapsförråd som möjligt bör vi söka efter ett enklare analogt problem. Här uppkommer helt naturligt motsvarande problem inom plangeometrin: Sök tyngdpunkten i en homogen triangel.
Nu har vi två frågor i stället för en. Men två frågor kan vara lättare att besvara än en fråga — förutsatt att de två frågorna har samband på ett intelligent sätt.
4. Vi bortser ett ögonblick från vårt ursprungliga problem med tetraedern och koncentrerar oss på det enklare analoga problemet med triangeln. För att lösa det problemet måste vi veta någonting om tyngdpunkt. Följande princip är då tänkbar. Om ett system av massor S består av delar, vilkas tyngdpunkt alla ligger i samma plan, så innehåller detta plan också tyngdpunkten för hela systemet S.
| Fig.7 | 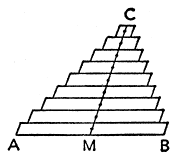 |
Denna princip ger oss allt vad vi behöver i fråga om triangeln. För det första så anger den att triangelns tyngdpunkt ligger i triangelns plan. För det andra kan vi anta att triangeln består av fibrer (tunna strimlor, "oändligt smala" parallellogrammer) parallella med en viss sida av triangeln (sidan AB i fig. 7). Tyngdpunkten för varje fiber (för varje parallellogram) är uppenbarligen dess mittpunkt och alla dessa mittpunkter ligger på den linje som förenar hörnet C med mittpunkten M av motstående sidan AB (se fig. 7).
Varje plan som går genom medianen CM i triangeln innehåller tyngdpunkten för alla parallella fibrer som utgör triangeln. Vi kommer alltså till slutsatsen att hela triangelns tyngdpunkt ligger på samma median. Eftersom den dessutom också måste ligga någonstans på de andra två medianerna måste den tydligen utgöras av de tre medianernas gemensamma skärningspunkt.
Det vore nu önskvärt att med hjälp av ren geometri, oberoende av några fysikaliska antaganden, bevisa att alla tre medianerna skär varandra i samma punkt.
5. Efter fallet med triangeln är fallet med tetraedern ganska lätt att lösa. Vi har nu löst ett problem som är analogt med det givna problemet, och eftersom vi har löst det har vi en modell att följa.
När vi löste det analoga problemet, som vi nu använder som modell, föreställde vi oss att triangeln ABC bestod av fibrer parallella med en av dess sidor, AB. Nu tänker vi oss att tetraedern ABCD består av fibrer parallella med en av dess kanter, AB.
| Fig.8 | 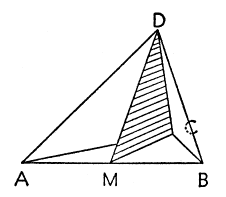 |
Mittpunkterna på de fibrer som utgör triangeln ligger alla på samma räta linje, en median i triangeln som förenar mittpunkten M av sidan AB med motstående hörn C. Mittpunkterna på de fibrer som utgör tetraedern ligger alla i samma plan, nämligen det som förenar mittpunkten M på kanten AB med motsatta kanten CD (se fig. 8). Vi kan kalla detta plan MCD ett medianplan i tetraedern.
När det gällde triangeln hade vi tre medianer likadana som MC, som var och en måste innehålla triangelns tyngdpunkt. Därför måste dessa tre medianer ha en punkt gemensam, vilken just är tyngdpunkten. För tetraedern har vi sex medianplan likadana som MCD, som förbinder mittpunkten på en kant med motstående kant, och vilka alla måste innehålla tetraederns tyngdpunkt. Därför måste dessa sex medianplan ha en punkt gemensam och den punkten är just tyngdpunkten.
6. Vi har alltså löst problemet med tyngdpunkten i en homogen tetraeder. För att fullborda lösningen vore det önskvärt att med ren geometri, oberoende av fysikaliska resonemang, bevisa att de sex medianplanen också går genom samma punkt.
När vi hade löst problemet med tyngdpunkten i en homogen triangel fann vi det önskvärt för att fullborda vår lösning att bevisa att de tre medianerna i triangeln passerar genom samma punkt. Detta problem är analogt med det föregående men betydligt enklare.
När vi löser problemet med tetraedern kan vi på nytt använda det motsvarande enklare analoga problemet med triangeln (som här skall antas vara löst). Betrakta nu de tre medianplan som går genom de tre kanterna DA, DB och DC, som utgår från hörnet D. Vart och ett skär mittpunkten på motsatta sidan (medianplanet genom DC går genom M, se fig. 8). Dessa tre medianplan skär triangeln ABC i dess tre medianer. Dessa tre medianer går genom samma punkt (det enklare, analoga problemets resultat) och denna punkt är liksom D en gemensam punkt för de tre medianplanen. Den räta linje som förbinder de två gemensamma punkterna är tydligen gemensam för alla tre medianplanen.
Vi har alltså visat att av de sex medianplanen har de tre som utgår från hörnet D en gemensam rät linje. Samma sak måste gälla om de tre medianplan som utgår från A och också om de tre medianplan som utgår från B liksom om de tre som utgår från C. Kombinerar vi dessa fakta på ett lämpligt sätt kan vi visa att de sex medianplanen har en gemensam punkt. (De tre medianplan som går genom sidorna av triangeln ABC bestämmer en gemensam punkt och tre skärningslinjer som möts i den gemensamma punkten. Men enligt vad vi nyss har visat måste genom varje skärningslinje gå ytterligare ett medianplan.)
7. Både under avsnitt 5 och 6 använde vi ett enklare analogt problem rörande triangeln för att lösa ett problem rörande tetraedern. Emellertid skiljer sig de två fallen i ett väsentligt avseende. I avsnitt 5 använde vi det enklare analoga problemets metod och imiterade lösningen punkt för punkt. I avsnitt 6 använde vi det enklare analoga problemets resultat, och vi brydde oss inte om hur vi hade kommit till detta resultat. Ibland kan vi använda både metoden och resultatet från det enklare analoga problemet. Även detta visar vårt föregående exempel om vi betraktar resonemangen under avsnitt 5 och 6 som skilda delar av lösningen till samma problem.
Vårt exempel är typiskt. När vi löser ett givet problem kan vi ofta använda lösningen till ett enklare analogt problem. Vi kan kanske använda metoden eller resultatet eller bådadera. Fast det inte framgick av vårt exempel kan komplikationer naturligtvis inträffa i svårare fall. Framför allt kan det inträffa att det analoga problemets lösning inte omedelbart kan tillämpas på vårt ursprungliga problem. Då kan det löna sig att ompröva lösningen, att variera och modifiera den tills vi, efter att ha prövat olika former på lösningen, slutligen finner någon som kan överföras till vårt ursprungliga problem.
8. Det är lämpligt att med någon grad av säkerhet försöka förutse resultatet eller åtminstone några karakteristiska grunddrag i resultatet. Sådana förutsägelser baseras ofta på analogier.
Kanske vet vi att tyngdpunkten i en homogen triangel sammanfaller med tyngdpunkten för dess tre hörn (dvs. för tre materiella punkter med lika massor placerade i triangelns hörn). Härav kan vi gissa att tyngdpunkten i en homogen tetraeder sammanfaller med tyngdpunkten för dess fyra hörn.
Denna gissning är en "slutsats baserad på analogi". Eftersom vi vet att triangeln och tetraedern liknar varandra i många avseenden förmodar vi att de liknar varandra i ännu ett avseende. Det skulle vara felaktigt att betrakta graden av möjlighet hos sådana gissningar som övertygande eller säker, men det skulle vara lika felaktigt eller ännu mera felaktigt att inte alls använda sig av dem.
Slutsats baserad på analogi tycks vara den vanligaste typen av slutsatser och den är förmodligen den viktigaste. Den leder till mer eller mindre säkra gissningar som antingen bekräftas eller inte bekräftas av erfarenhet och strängt logiska resonemang. Kemisten som experimenterar med djur för att försöka förutse drogers inverkan på människor drar slutsatser baserade på analogi. Men det gjorde också en liten pojke som jag kände. Hans knähund måste föras till veterinären och han frågade:
"Vad är veterinärn för en?"
"Djurdoktorn."
"Vilket djur är djurdoktorn?"
9. En analogiek slutsats härledd från många parallellfall är starkare än en från ett fåtal fall. Ändå betyder kvalitet här fortfarande mer än kvantitet. Klara analogier väger tyngre än vaga likheter, systematiskt insamlade exempel är värda mera än slumpvise fall.
Vi framställde ovan (under avsnitt 8) en gissning om tyngdpunkten i en tetraeder. Denna gissning understöddes genom analogi. Fallet med tetraedern är analogt med fallet med triangeln. Vi kan förstärka vår förmodan genom att undersöka ännu ett analogt fall, fallet med en homogen stav (dvs, ett rätlinjigt segment med likformig täthet). Analogin mellan segment — triangel — tetraeder har många aspekter. Ett segment är inbäddat i en rät. linje, en triangel i ett plan, en tetraeder i rymden. Ett rätlinjigt segment är den enklaste endimensionella, begränsade figuren, triangeln den enklaste polygonen, tetraedern den enklaste polyedern.
Segmentet har två nolldimensionella begränsningselement (två ändpunkter) och dess inre är endimensionellt.
Triangeln har tre nolldimensionella och tre endimensionella begränsningselement (tre hörn, tre sidor) och dess inre är tvådimensionellt.
Tetraedern har fyra nolldimensionella, sex endimensionella och fyra tvådimensionella begränsningselement (fyra hörn, sex kanter, fyra ytor) och dess inre är tredimensionellt.
Av dessa tal kan vi göra en tabell. Kolumnerna anger i tur och ordning antalet 0-, 1-, 2- och 3-dimensionella element, och raderna gäller för segment, triangel och tetraeder uppifrån räknat.
| 2 | 1 | ||
| 3 | 3 | 1 | |
| 4 | 6 | 4 | 1 |
Bara någon kännedom om binomialteoremet behövs för att känna igen en del av Pascals triangel i dessa tal. Vi har här funnit en anmärkningsvärd regelbundenhet när vi går från segment till triangel och tetraeder.
10. Om vi har funnit att de fall vi jämför är nära relaterade kan "slutsatser baserade på analogi", som de följande, vara av ett visst värde för oss.
Tyngdpunkten i en homogen stav sammanfaller med tyngdpunkten för dess två ändpunkter. Tyngdpunkten i en homogen triangel sammanfaller med tyngdpunkten för dess tre hörn. Borde vi inte ha rätt att misstänka att tyngdpunkten i en homogen tetraeder sammanfaller med tyngdpunkten för dess fyra hörn?
Tyngdpunkten i en homogen stav delar sträckan mellan dess ändpunkter i förhållandet 1:1. Tyngdpunkten i en triangel delar avståndet mellan varje hörn och mittpunkten av den motsatta sidan i förhållandet 2:1. Borde vi inte ha rätt att misstänka att tyngdpunkten i en homogen tetraeder delar avståndet mellan varje hörn och motstående sidas tyngdpunkt i förhållandet 3:1?
Det förefaller ytterst osannolikt att de gissningar som ligger i dessa frågor skulle vara felaktiga och att en sådan skön regelbundenhet skulle förstöras. Känslan att en harmonisk enkel ordning inte kan vara felaktig leder forskaren både i matematik och i andra vetenskaper och uttrycks av den latinska sentensen: Simplex sigilltim veri (Enkelhet är sanningens kännetecken).
[Det föregående antyder att resonemanget kan utsträckas till n dimensioner. Det förefaller osannolikt att vad som är sant i de tre första dimensionerna, för n = 1, 2, 3, skulle upphöra att vara sant för högre värden på n. Denna gissning är en "slutsats genom induktion" en illustrerar att induktion vanligtvis är baserad på analogi. Se Induktion och matematisk induktion.]
[11. Vi avslutar detta avsnitt med att i korthet betrakta de viktigaste fall i vilka analogi uppnår de matematiska idéernas precision.
a) Två system av matematiska objekt, S och S', är besläktade i den meningen att vissa relationer mellan objekten i S styrs av samma lagar som motsvarande relationer mellan objekten i S'.
Detta slags analogi mellan S och S' exemplifieras av vad vi förut har diskuterat under avsnitt 1. S är där sidorna i en rektangel, S' ytorna i en rektangulär parallellepiped.
b) Det finns en "en till en-korrespondens" mellan objekten i de två systemen S och S', som bevarar vissa relationer. Detta innebär att om en sådan relation gäller mellan objekten i det ena systemet så gäller samma relation mellan motsvarande objekt i det andra systemet. En sådan släktskap mellan två system är ett mycket precist slag av analogi. Den kallas isomorfism (eller holoedrisk isomorfism).
c) Det finns en "en till flera-korrespondens" mellan objekten i de två systemen S och S', som bevarar vissa relationer. En sådan släktskap (som är viktig i olika grenar av avancerad matematik, speciellt inom gruppteorin, men som inte behöver diskuteras i detalj här) kallas meroedrisk isomorfism (eller homomorfism; homoisomorfism skulle kanske vara en bättre term). Meroedrisk isomorfism kan anses vara ett annat mycket precist slag av analogi.]
Använde du alla de givna uppgifterna? Genom att en allt större del av våra kunskaper kommer till användning ju längre lösningen av ett problem framskrider, är vår uppfattning om problemet mycket mera innehållsrik på slutet än den var i början (Framsteg och prestation, 1). Men hur ser den ut nu? Har vi vad vi behöver? Är vår uppfattning tillräcklig? Använde du alla de givna uppgifterna? Använde du hela villkoret? Motsvarande fråga beträffande "bevisproblem" är: Använde du hela antagandet?
1. Låt oss för att få ett belysande exempel gå tillbaka till problemet med parallellepipeden i avsnitt 8 (vidare utvecklat i avsnitt 10, 12, 14, 15). Det kan mycket väl hända att en elev kommer på idén att beräkna diagonalen i en yta, ![]() , men sedan kör fast. Läraren kan hjälpa honom genom att fråga: Använde du alla de givna uppgifterna? Eleven kan knappast undgå att lägga märke till att uttrycket
, men sedan kör fast. Läraren kan hjälpa honom genom att fråga: Använde du alla de givna uppgifterna? Eleven kan knappast undgå att lägga märke till att uttrycket ![]() inte innehåller den tredje givna storheten c. Därför måste han försöka få med c i bilden. I så fall finns det stora möjligheter att han lägger märke till den avgörande rätvinkliga triangel vilkens sidor är
inte innehåller den tredje givna storheten c. Därför måste han försöka få med c i bilden. I så fall finns det stora möjligheter att han lägger märke till den avgörande rätvinkliga triangel vilkens sidor är ![]() och c och vilkens hypotenusa utgör den sökta diagonalen i parallellepipeden. (För ytterligare exempel se
Hjälpkonstruktioner, 3.)
och c och vilkens hypotenusa utgör den sökta diagonalen i parallellepipeden. (För ytterligare exempel se
Hjälpkonstruktioner, 3.)
De frågor vi diskuterar här är mycket viktiga. Hur de används vid uppbyggandes av en lösning visas klart av föregående exempel. De kan hjälpa oss att finna den svaga punkten i vår uppfattning om problemet. De kan påvisa ett felande element. Om vi vet att en viss storhet saknas försöker vi naturligtvis föra in den i bilden. Där har vi alltså en ledtråd. Vi har en bestämd linje att fråga vidare på och vi har en god chans att träffa på den avgörande idén.
2. De frågor vi diskuterade är användbara inte bara när det gäller att konstruera ett argument utan också när det gäller att kontrollera det. Låt oss för att vara mer konkreta anta att vi skall kontrollera beviset till en sats vars antagande består av tre delar. Alla tre är väsentliga för satsens giltighet, dvs, om vi bortser från någon del av antagandet upphör satsen att vara sann. Om man nu för beviset utelämnar någon del av antagandet måste beviset vara felaktigt. Används hela antagandet i beviset? Används första delen av antagandet? Var används antagandets första del? Var används andra delen? Var den tredje? Genom att besvara alla dessa frågor kontrollerar vi beviset.
Denna typ av kontroll är effektiv, instruktiv och nästan nödvändig för att man skall få full insikt om argumenteringen är lång och tung — något som Den intelligente läsaren bör veta.
3. Syftet med de frågor vi diskuterade är att undersöka hur fullständig vår uppfattning om problemet är. Vår uppfattning är säkerligen ofullständig om vi försummar att ta med i beräkningen någon viss nödvändig given storhet eller något nödvändigt villkor eller antagande. Men den är också ofullständig om vi inte förstår innebörden av något nödvändigt begrepp. För att undersöka vår uppfattning om problemet bör vi därför även fråga: Har du tagit hänsyn till alla nödvändiga begrepp som ingår i problemet? Se Definition, 7.
4. Ovanstående påpekanden måste emellertid användas med försiktighet och de har vissa begränsningar. I själva verket kan de direkt tillämpas endast i problem som är "idealiskt formulerade" och "rimliga".
Ett idealiskt formulerat och rimligt "sökproblem" måste innehålla alla uppgifter som är nödvändiga men får inte innehålla någon enda överflödig uppgift. Dessutom måste dess villkor vara precis tillräckligt, varken motsägelsefullt eller överflödigt. När vi löser ett sådant problem måste vi naturligtvis använda alla givna uppgifter och hela villkoret.
Det som behandlas i ett "bevisproblem" är en matematisk sats. Om problemet är idealiskt formulerat och rimligt måste varje del av antagandet i satsen vara nödvändig för påståendet. När vi bevisar en sådan sats måste vi naturligtvis använda varje del av antagandet.
De matematiska problem som förekommer i traditionella läroböcker antas vara idealiskt formulerade och rimliga. Vi bör emellertid inte lita för mycket på detta. Finns det minsta anledning att vara tveksam bör vi i stället fråga oss: Är det möjligt att uppfylla villkoret? Om vi försöker besvara denna eller någon liknande fråga kan vi åtminstone i viss utsträckning komma underfund med om problemet är så bra som det antas vara.
Frågan i rubriken till denna artikel och frågor som hör ihop med den kan och bör ställas utan att ändras endast när vi vet att det problem vi har framför oss är rimligt och idealiskt formulerat eller när vi åtminstone inte har några skäl att misstänka motsatsen.
5. Det finns några icke-matematiska problem som i en viss mening kan vara "idealiskt formulerade". Ett bra schackproblem t.ex. antas ha endast en lösning och ingen överflödig pjäs på schackbrädet.
Praktiska problem är emellertid vanligen långt ifrån idealiskt formulerade och kräver därför en grundlig omprövning av de frågor som diskuteras i denna artikel.
Att arbeta baklänges. Om vi vill förstå människans beteende så bör vi jämföra det med djurens beteende. Även djur "har problem" och "löser problem". Den experimentella psykologin har gjort avsevärda framsteg under de sista decennierna när det gäller att utforska den "problemlösande" verksamheten hos olika djurarter. Vi kan inte här diskutera dessa undersökningar men vi skall i korthet skissera ett enkelt och lärorikt experiment. Vår beskrivning kommer att tjäna som ett slags kommentar till analysmetoden eller metoden att "arbeta baklänges". Metoden diskuteras för övrigt även under avsnittet Pappus, vilken vi har att tacka för en viktig beskrivning av metodena
1. Låt oss försöka finna ett svar på följande knepiga fråga: Hur kan man hämta upp exakt sex liter vatten ur en flod när man bara har två behållare att mäta med, den ena en spann om fyra, den andra om nio liter?
| Fig.9 | 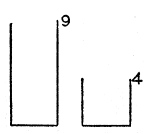 |
Låt oss åskådliggöra de givna verktyg vi har att arbeta med, de två behållarna. (Vad är det som är givet?) Vi föreställer oss två cylindriska behållare som har samma bottenyta och vars höjder förhåller sig som 9:4 (se fig. 9). Om vi hade haft en skala med likformigt fördelade horisontella linjer utefter sidan på vardera behållaren, skulle vi kunna avläsa vattenlinjens höjd och vårt problem skulle vara lätt. Men det finns ingen sådan skala och vi är därför ännu långt ifrån lösningen.
Vi vet ännu inte hur man kan mäta upp exakt 6 liter, men skulle vi kunna mäta någonting annat? (Om du inte kan lösa det givna problemet, försök först lösa något liknande problem. Skulle du kunna härleda någonting användbart ur de givna uppgifterna?) Låt oss göra någonting, låt oss leka litet grann. Vi skulle kunna fylla den större behållaren till brädden och tömma så mycket vi kan i den mindre behållaren. Då skulle vi få 5 liter kvar. Skulle vi också kunna få 6 liter? Här har vi igen de två tomma behållarna. Vi skulle också kunna …
Nu arbetar vi som de flesta människor gör när de konfronteras med ett sådant här problem. Vi börjar med de två tomma behållarna, vi försöker än det ena och än det andra, vi tömmer och fyller på, och när det inte lyckas så börjar vi från början och försöker någonting annat. Vi arbetar framlänges, från den givna begynnelsesituationen till den önskade slutsituationen, från det som är givet till det som söks. Kanske lyckas vi genom en lyckträff efter många försök.
| Fig. 10 | 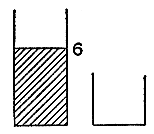 |
| Fig. 11 | 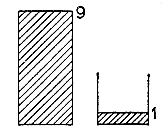 |
2. Men mycket begåvade personer eller personer som har haft möjlighet att lära sig någonting mer än rena rutinoperationer i matematikundervisningen använder inte för mycket tid på sådana försök utan vänder på kakan och börjar arbeta baklänges.
Vad är det som begärs? (Vad är det som söks?) Låt oss åskådliggöra så klart som möjligt den slutliga situation vi söker. Vi föreställer oss att vi framför oss har den större behållaren fylld med exakt 6 liter och den mindre behållaren tom som i fig. 10. (Låt oss börja från det som begärs och anta att vi redan har funnit det som söks, säger Pappus.)
Från vilken föregående situation skulle vi kunna uppnå den önskade slutsituationen i fig. 10? (Låt oss undersöka ur vilken omedelbart föregående situation det önskade resultatet skulle kunna härledas, säger Pappus.) Vi skulle naturligtvis kunna fylla den större behållaren till brädden, dvs. till 9 liter. Men i så fall måste vi också kunna hälla ut exakt 3 liter. Och för att göra det … måste vi ha exakt en liter i den mindre behållaren! Där har vi idén. Se fig. 11.
(Det resonemang vi just har avslutat är inte alls lätt. Få personer kan föra det utan att först tveka länge. När vi inser betydelsen av resonemanget innebär det i själva verket att vi förutser hur den följande lösningen kommer att se ut.)
| Fig. 12 | 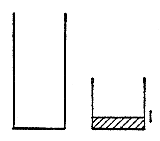 |
| Fig. 13 | 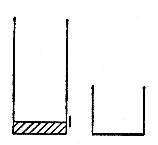 |
| Fig. 14 | 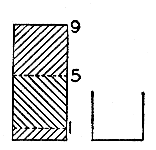 |
Men hur kan vi komma till den situation som vi nyss beskrivit och som är illustrerad i fig. 11? (Låt oss undersöka igen vad som skulle kunna föregå det föregående.) Eftersom mängden vatten i floden är obegränsad för vårt ändamål är situationen i fig. 11 ekvivalent med den i fig. 12 eller den i fig. 13.
Det är lätt att se att om vi har kommit fram till någon av situationerna i fig. 11, 12 eller 13, så kan vi omedelbart erhålla de andra. Men det är inte så lätt att se hur vi kommer till situationen i fig. 13, såvida vi inte har sett den förr, har träffat på den rent händelsevis i något av våra tidigare försök. Kanske gjorde vi någonting liknande när vi tidigare lekte med de två behållarna, och nu kommer vi ihåg i det rätta ögonblicket att situationen i fig. 13 kan uppstå på det sätt som antyds i fig. 14.
Vi fyller den stora behållaren till brädden och tömmer 4 liter därav i den mindre behållaren som vi därefter tömmer i floden. Detta gör vi 2 gånger i följd. Slutligen träffade vi på någonting redan känt (detta är Pappus' ord), och genom en analys där vi arbetade baklänges har vi upptäckt den riktiga följden av åtgärder.
Det är visserligen sant att vi har fått fram de rätta åtgärderna i omvänd ordningsföljd men allt som behöver göras nu är att vända processen och utgå från den punkt som vi nått sist i analysen (som Pappus uttrycker det). Först utför vi de operationer som antyds av fig. 14 och erhåller fig. 13. Sedan går vi till fig. 12, därefter till fig. 11 och slutligen till fig. 10. Genom att vända om samma väg lyckas vi slutligen härleda det som begärdes.
3. Den grekiska traditionen tillskriver Platon upptäckten av den analytiska metoden. Traditionen kanske inte är helt tillförlitlig men om metoden inte infördes av Platon så fann i vilket fall som helst någon grekisk lärd det nödvändigt att tillskriva ett filosofiskt geni denna upptäckt.
Det finns säkerligen någonting i metoden som inte är ytligt. Det innebär en viss psykologisk svårighet att vända på kakan, att avlägsna sig från målet, att arbeta baklänges, att inte följa den raka vägen till det önskade målet. När vi upptäcker följden av lämpliga åtgärder måste våra tankar fortsätta i en riktning som är rakt motsatt jämförd med den i vilken åtgärderna i verkligheten vidtas. Det finns ett slags psykologisk motvilja mot denna omvända ordning som mycket väl kan hindra en begåvad elev från att förstå metoden, om den inte beskrivs på ett omsorgsfullt sätt.
Ändå behöver man inte vara ett geni för att lösa ett konkret problem genom att arbeta baklänges. Vem som helst kan göra det med litet sunt förnuft. Vi koncentrerar oss på det önskade målet, vi föreställer oss den slutliga situation som vi skulle vilja befinna oss i. Från vilken föregående situation kan vi komma dit? Det är naturligt att ställa denna fråga, och när vi gör det arbetar vi baklänges. Mycket enkla problem leder naturligen till detta arbetssätt; se Pappus, 4.
Att arbeta baklänges är en det sunda förnuftets metod som var och en kan komma på och vi behöver knappast tvivla på att den tillämpades av matematiker och icke-matematiker före Platon. Det som grekiska lärda förmodligen betraktade som en bedrift värdig Platons geni var att ge metoden en allmän formulering och att anföra den som en operation vilken normalt är användbar när man löser matematiska och icke-matematiska problem.
| Fig. 15 | 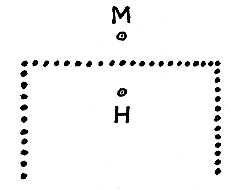 |
4. Och nu vänder vi oss till det psykologiska experimentet — om övergången från Platon till hundar, höns och schimpanser inte förefaller läsaren för abrupt. Ett staket bildar tre sidor i en rektangel och lämnar därvid den fjärde sidan öppen som i fig. 15. Vi placerar en hund på ena sidan av staketet, vid punkten H, och litet mat på andra sidan, vid punkten M. Problemet är ganska lätt för en hund. Han kanske först intar en kroppsställning som om han ville hoppa över direkt till maten men strax vänder han om, rundar staketet och når maten utan att tveka genom att springa i en båge. Ibland blir förloppet emellertid inte så elegant, speciellt om punkterna H och M ligger nära varandra. Hunden kanske då spiller tid genom att skälla, gräva med tassarna eller hoppa mot staketet innan han "får den ljusa idén" (som vi skulle uttrycka det) att gå runt det.
Det är intressant att jämföra hur olika djur uppträder i hundens ställe. Problemet är mycket lätt för en schimpans eller ett fyra års barn (för vilket en leksak kanske är mera attraktiv än mat). Däremot visar sig problemet vara förvånansvärt svårt för en höna, som vimsigt springer fram och tillbaka på sin sida av staketet och kan tillbringa åtskillig tid innan hon får tag på födan om hon kommer till den över huvud taget. Men hon kanske lyckas rent händelsevis efter mycket springande.
5. Vi bör inte formulera en viktig teori efter ett enda enkelt experiment som har refererats endast skissartat. Likväl kan det inte vara till någon nackdel att försöka finna uppenbara analogier förutsatt att vi är beredda att ompröva och omvärdera dem.
Att gå runt ett hinder är vad vi gör när vi löser varje slag av problem. Experimentet har ett slags symboliskt värde. Hönan gjorde som folk som löser sina problem genom att arbeta på måfå och försöka gång på gång, och som slutligen lyckas genom någon lycklig tillfällighet utan att egentligen förstå varför de lyckades. Hunden som grävde med tassarna och hoppade och skällde innan han rusade runt löste sitt problem ungefär lika bra som vi löste vårt med de två behållarna. Att föreställa sig en skala som visar vattenlinjen i våra behållare var ju ett slags hopplöst grävande, som bara visade att det vi sökte låg djupare än så. Vi försökte också först att arbeta framlänges och kom senare på idén att vända på kakan. Hunden som vände om och rusade runt efter att först snabbt ha överblickat situationen ger med rätt eller orätt intryck av överlägset förstånd.
Nej, vi hör inte ens klandra hönan för hennes vimsighet. Det ligger en viss svårighet i att vända om, att avlägsna sig från målet, att fortsätta utan att hela tiden ha målet i sikte, att inte följa den raka vägen till det önskade målet. Det finns en uppenbar analogi mellan hönans svårigheter och våra.
Att genomföra planen. Att tänka ut en plan och att genomföra den är två helt olika saker. Detta gäller i en viss mening också matematiska problem. Med hänsyn till arbetets karaktär finns det vissa skillnader mellan att tänka ut en plan för en lösning och att genomföra den.
1. Vi kan använda tillfälliga och enbart rimliga argument när vi tänker ut det slutgiltiga och strängt logiska argumentet ungefär som vi använder stöttor vid ett brobygge. När arbetet emellertid har fortskridit tillräckligt långt tar vi bort stöttorna och då skall bron kunna stå av sig själv. På samma sätt avlägsnar vi alla tillfälliga och enbart rimliga argument när vår matematiska lösning är tillräckligt långt framskriden. Resultatet skall då bäras upp enbart av strängt logiska argument.
När vi tänker ut planen för lösningen behöver vi inte vara alltför rädda för enbart rimlig, heuristisk argumentation. Allting är rätt som leder till den rätta idén. Men vi måste ändra denna inställning när vi börjar genomföra planen, och då får vi acceptera enbart avgörande, strängt logiska argument. När du genomför den plan som utformats för lösningen så kontrollera varje steg. Kan du klart se att steget är korrekt?
Ju mer noggrant vi kontrollerar varje steg när vi genomför planen, desto friare kan vi använda heuristiska argument när vi gör upp planen.
2. Vi måste ägna någon uppmärksamhet åt den ordning i vilken detaljerna av planen skall utarbetas, speciellt om problemet är komplicerat. Vi får inte bortse från någon detalj, vi måste förstå hur varje detalj förhåller sig till hela problemet, vi får inte förlora överblicken över de stora stegen och deras samband. Vi måste därför arbeta i riktig ordning.
Framför allt är det inte lämpligt att kontrollera mindre detaljer innan vi har goda skäl att anta att de stora dragen i vår argumentation är hållbara. Om det finns någon lucka i resonemangets huvuddrag är det naturligtvis meningslöst att kontrollera mindre betydelsefulla detaljer.
Den ordning efter vilken vi utarbetar argumentationens detaljer kan skilja sig mycket från den ordning i vilken vi kom på den. Ordningen kan vara ytterligare en annan när vi skriver ner detaljerna i en slutgiltig framställning. Euklides Elementa presenterar argumentationens detaljer i en strängt systematisk ordning som ofta har imiterats och kritiserats.
3. I Euklides framställning förs all argumentation i samma riktning: från det som är givet mot det som är okänt i ett "sökproblem" och från antagandet mot påståendet i ett "bevisproblem". Varje nytt element, punkt, linje etc., måste härledas på ett korrekt sätt från det som är givet eller ur de element som likaledes korrekt har härletts i tidigare steg. Varje nytt påstående måste bevisas ur antagandet eller från påståenden som har bevisats i tidigare steg. Varje nytt element, varje nytt påstående undersöks när det uppträder första gången och behöver därför undersökas endast en gång. Vi kan därigenom koncentrera all vår uppmärksamhet på det aktuella steget och behöver inte titta bakåt och inte framåt. Det allra sista nya elementet vars härledning vi måste kontrollera är den obekanta. Det allra sista påståendet vars bevis vi måste undersöka är satsens hela påstående. Om varje steg är korrekt, även det sista, är hela argumentationen korrekt.
Euklides framställningssätt kan rekommenderas utan reservation i allra högsta grad om syftet är att undersöka argumentationen i detalj. Framför allt om det är vår egen argumentation och om den är lång och komplicerad, och om vi inte bara funnit den utan även granskat den i sina huvuddrag så att ingenting återstår utom att undersöka varje särskild del i den, finns ingenting bättre än att skriva ut hela argumentationen på det euklidiska sättet.
Euklides framställningssätt kan emellertid inte rekommenderas utan vidare om syftet är att överföra en argumentation till en läsare eller en lyssnare som aldrig har hört talas om den förut. Euklides framställningssätt är utmärkt för att visa varje särskild punkt men sämre när det gäller att visa argumentationens huvudlinje. Den intelligente läsaren kan med lätthet se att varje steg är korrekt men får stora svårigheter att uppfatta orsaken till, syftet med och sambandet i hela argumentationen. Skälet till denna svårighet är att Euklides framställning ganska ofta framskrider i en ordning som är precis motsatt den naturliga gången vid upptäckter. (Euklides framställning följer strängt ordningen i en "syntes". Se Pappus, framför allt avsnitt 3, 4, 5.
4. Låt oss summera. Euklides sätt att obevekligt röra sig framåt från det som är givet mot det som söks och från antagandet mot påståendet är perfekt för att kontrollera en argumentation i detalj men långt ifrån perfekt för att klargöra huvudlinjen i en argumentation.
Det är synnerligen lämpligt att låta eleverna undersöka sina egna argument på det euklidiska sättet och gå från det givna till det sökta varvid varje steg kontrolleras. Likväl bör man inte hålla för hårt på detta. Det är emellertid inte så lämpligt att läraren presenterar bevis på det rent euklidiska sättet. Euklides framställning kan dock vara mycket användbar efter en diskussion, i vilken eleverna själva så oberoende som möjligt men under ledning av läraren får upptäcka huvudidén i en lösning, något som rekommenderas i denna bok. En metod som används i några läroböcker och som också verkar mycket lämplig är att först ge en intuitiv skiss av den huvudsakliga idén och därefter framställa detaljerna på det euklidiska sättet.
5. Den samvetsgranne matematikern som vill övertyga sig själv om att hans påstående är sant försöker både att se det intuitivt och att ge ett formellt bevis. Kan du klart se att detta är korrekt? Kan du bevisa att det är riktigt? Den samvetsgranne matematikern handlar i detta avseende precis som den som är noga med sina inköp. Då man vill övertyga sig om en varas kvalitet vill man både se den och känna på den. Intuitiv insikt och formell bevisföring är två olika metoder att komma fram till sanningen, jämförbara med förnimmelsen av ett materiellt föremål genom två olika sinnen, synen och känseln.
Intuitionen kan rusa iväg långt före ett formellt bevis. Vilken intelligent elev som helst utan några som helst systematiska kunskaper i rymdgeometri inser, så snart han förstår facktermerna, att två linjer som är parallella med samma räta linje också är parallella med varandra (de tre linjerna kan ligga i samma eller olika plan). Likväl kräver beviset för detta påstående, så som det ges i sats 9 i elfte boken av Euklides Elementa, en lång, omsorgsfull och djupgående förberedelse.
Tekniskt manipulerande med logiska regler och algebraiska formler kan rusa långt före intuitionen. Nästan vem som helst ser omedelbart att tre räta linjer valda på måfå delar planet i sju delar (titta på den enda ändliga delen, triangeln som omsluts av de tre linjerna). Knappast någon kan ens med yttersta ansträngning se att fem plan valda på måfå delar rummet i 26 delar. Ändå kan det bevisas att det rätta antalet faktiskt är 26. Beviset är inte ens långt eller svårt.
När vi genomför vår plan kontrollerar vi varje steg. När vi kontrollerar ett steg kan vi lita på intuition eller på formella regler. Ibland kommer intuitionen först, ibland det formella resonemanget. Det är en intressant och nyttig övning att göra det på båda sätt. Kan du klart se att steget är korrekt? Ja, jag ser det klart och tydligt. Intuitionen ligger före, men skulle ett formellt resonemang kunna gå förbi, komma längre? Kan du också bevisa att det är riktigt?
Att försöka bevisa formellt vad man ser intuitivt och att se intuitivt vad som har bevisats formellt är en stärkande tankeövning. Tyvärr finns det inte alltid tillräckligt med tid för sådant i en klass. Det exempel som diskuteras i avsnitt 12 och 14 är typiskt i detta avseende.
Att ställa upp ekvationer är som att översätta från ett språk till ett annat (Notation, 1). Denna jämförelse som användes av Newton i hans arithmetica universalis kan bidra till att klargöra arten av vissa svårigheter som både studenter och lärare ofta ställs inför.
1. Att ställa upp en ekvation innebär att i matematiska symboler uttrycka ett villkor som är givet med ord. Ekvationen är en översättning från vanligt språk till matematikens formelspråk. De svårigheter vi kan möta när vi ställer upp ekvationer är översättningssvårigheter.
För att kunna översätta en mening från svenska till engelska fordras två saker. För det första måste vi klart förstå den svenska meningen. För det andra måste vi grundligt känna till de uttrycksformer som är speciellt karakteristiska för det engelska språket. Situationen är nästan densamma när vi i matematiska symboler försöker uttrycka ett villkor formulerat i ord. För det första måste vi förstå villkoret ordentligt. För det andra måste vi grundligt känna till formerna för matematiska uttryck.
En svensk mening är ganska lätt att översätta till engelska om den kan översättas ord för ord. Men det finns svenska uttryck som inte går att översätta ord för ord. Om vår mening innehåller många sådana uttryck blir översättningen besvärlig. Vi får ta mindre hänsyn till de enskilda orden och titta mer på meningens innebörd. Innan vi översätter meningen kanske vi måste ordna om den.
Förhållandena är likartade när vi ställer upp ekvationer. I lätta fall kan en uppgift i ord nästan automatiskt delas upp i delar som var och en omedelbart kan översättas till matematiska symboler. I svårare fall har villkoret delar som inte utan vidare kan skrivas i matematiska symboler. Om det förhåller sig så måste vi bortse från den ordagranna lydelsen i uppgiften och koncentrera oss på dess innebörd. Innan vi börjar skriva formler kanske vi måste ordna om villkoret, och medan vi gör det skall vi hålla ögonen på vilka matematiska beteckningssätt vi har att tillgå.
I samtliga fall, lätta som svåra, måste vi förstå villkoret, dela upp villkorets olika delar, och fråga: Kan man skriva ner dem? I lätta fall lyckas vi utan svårighet dela upp villkoret i delar som kan uttryckas i matematiska symboler. I svårare fall är en lämplig uppdelning av villkoret mindre uppenbar.
Det föregående hör läsas igen efter studium av följande exempel.
2. Sök de två storheter vars summa är 78 och vars produkt är 1296.
Vi drar en lodrät linje mitt på sidan. Till vänster skriver vi uppgiften i ord uppdelad i lämpliga delar. Till höger skriver vi de algebraiska tecknen mittemot motsvarande del av uppgiften i ord.
| i ord | på algebraiska språk | |
| Sök de två storheter | x, y | |
| vars summa är 78 och | x + y = 78 | |
| vars produkt är 1296 | xy = 1296 |
I detta fall kan uppgiften i ord nästan automatiskt delas upp i successiva delar som var och en omedelbart kan översättas till matematiska symboler.
3. Beräkna bredden och höjden av ett rakt prisma med kvadratisk bas om dess volym är 63 cm³ och dess yta 102 cm².
Vad är det som söks? Prismats bredd, låt oss kalla den x, och prismats höjd, låt oss kalla den y.
Vad är det som är givet? Volymen, 63, och ytan, 102.
Hur lyder villkoret? Det raka prismat med höjden y har en kvadratisk bas med sidan x och skall ha volymen 63 och ytan 102.
Dela upp villkorets olika delar. Det finns två delar. Den ena handlar om volymen, den andra om ytan.
Vi behöver knappast tveka om att dela upp villkoret i bara dessa två delar. Men vi kan inte skriva ner dessa delar "omedelbart". Vi måste veta hur man beräknar volymen och de olika delarna av ytan. Men om vi kan så pass mycket geometri kan vi lätt formulera om båda delarna av villkoret så att en översättning till ekvationer blir möjlig. Vi skriver då på vänstra delen av sidan en väsentligt omordnad och utvidgad formulering av problemet som nu är klart för översättning till algebra.
4. Antag att koordinaterna för en punkt och ekvationen för en rät linje är givna. Sök koordinaterna för den punkt som är symmetriskt belägen på andra sidan linjen.
Detta är ett problem i analytisk geometri.
Vad är det som söks? En punkt med koordinaterna (p, q).
Vad är det som är givet? Den räta linjens ekvation y = mx + n och en punkt med koordinaterna (a, b).
| I ett rakt prisma med kvadratisk bas, sök basens sida | x | |
| och höjden. | y | |
| För det första är volymen given. | 63 | |
| Ytan av den kvadratiska basen med sidan x | x² | |
| och höjden | y | |
| bestämmer volymen som är deras produkt. | x²y = 63 | |
| För det andra är prismats yta given. | 102 | |
| Ytan består av kvadrater med sidan x | 2 x² | |
| och av fyra rektanglar vardera med basen x och höjden y | 4 xy | |
| vilkas summa utgör ytan. | 2x² + 4xy = 102 |
Hur lyder villkoret? Punkterna (a, b) och (p, q) är symmetriskt belägna med avseende på linjen y = mx + n.
Vi kommer nu till den stora svårigheten att dela upp villkoret i delar som kan uttryckas i den analytiska geometrins språk. Det är nödvändigt att vi väl förstår arten av denna svårighet. En uppdelning av villkoret i delar kan vara logiskt oantastbar och lika fullt oanvändbar. Vad vi här behöver är en uppdelning i delar som passar för analytiskt uttryck. För att finna en sådan uppdelning måste vi gå tillbaka till definitionen av symmetri, samtidigt som vi håller ett öga på hur den analytiska geometrin kan hjälpa oss. Vad menas med symmetri med avseende på en rät linje? Vilka geometriska samband kan vi enkelt uttrycka med analytisk geometri? Vi koncentrerar oss på den första frågan utan att glömma den senare. Vi kanske då slutligen finner den uppdelning som vi nu skall formulera.
| Den givna punkten | (a, b) | |
| och den sökta punkten | (p, q) | |
| är relaterade så att för det första är linjen som förbinder dem vinkelrätt mot den givna linjen, |
||
| och för det andra ligger förbindelselinjens medelpunkt på den givna linjen. |
Beslutsamhet, hopp, framgång. Det skulle vara ett misstag att tro att problemlösning är en helt och hållet "intellektuell angelägenhet". Beslutsamhet och känslor spelar en betydelsefull roll. Ljum beslutsamhet och sömnigt samtycke att göra något vad som helst kan räcka för ett rutinproblem i ett klassrum. Men för att lösa ett allvarligt vetenskapligt problem krävs en viljestyrka som kan hålla under många år av slit och bittra besvikelser.
1. Beslutsamheten varierar med hopp och hopplöshet, med tillfredsställelse och besvikelse. Det är lätt att fortsätta arbeta när vi tror att lösningen ligger inom räckhåll, men det är svårt att hålla ut när vi inte ser någon väg ut ur svårigheterna. Vi känner oss uppmuntrade när våra förutsägelser slår in. Vi blir missmodiga när den väg vi optimistiskt har följt plötsligt blockeras. Vår beslutsamhet vacklar.
"Man kan företa sig något utan hopp och framhärda utan framgång." Så talar en oböjlig vilja, eller ära och plikt, eller en person med ett högt och ädelt syfte. Detta slags beslutsamhet skulle emellertid inte duga för en vetenskapsman, som behöver ha något hopp när han börjar och någon framgång för att kunna fortsätta. I vetenskapligt arbete är det nödvändigt att rätt avväga insatsen mot utsikt till framgång. Man skall inte ge sig in på ett problem såvida det inte har något intresse. Man fördjupar sig i allvarligt arbete om problemet verkar lärorikt. Man lägger ner hela sin själ om problemet är synnerligen lovande. Om syftet är klart håller man fast vid det, men man gör det inte onödigt svårt för sig. Man avvisar inte små framgångar, tvärtom, man söker dem: Om du inte kan lösa det givna problemet, försök först lösa något liknande problem.
2. När en elev begår verkligt enfaldiga misstag eller fattar förtvivlat långsamt är orsaken nästan alltid densamma. Han har ingen önskan att lösa problemet eller ens att förstå det, och därför har han inte heller förstått det. En lärare som verkligen vill hjälpa eleven måste därför framför allt väcka elevens nyfikenhet, få honom att önska att lösa problemet. Läraren bör också låta eleven få tid att bestämma sig, att börja vänja sig vid sin uppgift.
Att lära ut hur man löser problem är att uppfostra viljan. När en elev löser problem som inte är alltför lätta för honom lär han sig att hålla ut trots motgångar, att uppskatta små framsteg, att vänta på den rätta idén och att koncentrera sig allt vad han kan när idén kommer. Om eleven aldrig har fått tillfälle att i skolan erfara de känslor som infinner sig när man brottas med lösningen till ett problem har hans matematiska utbildning misslyckats på den viktigaste punkten.
Beteckningar och termer som beskriver processen att lösa problem är ofta tvetydiga. Processen som sådan är känd för var och en och diskuteras ofta men är som alla andra tankeaktiviteter svår att beskriva. Eftersom inga systematiska studier har gjorts finns det inga tekniska termer för att beskriva den, och vissa vanliga halvtekniska termer ökar ofta förvirringen eftersom de används i skilda betydelser av olika författare.
Följande korta lista innehåller några nya termer som används och några äldre termer som undviks i föreliggande framställning, och dessutom några äldre termer som har bibehållits trots deras tvetydighet.
Den följande behandlingen av terminologi kan mycket väl komma att förvirra läsaren såvida inte hans kunskaper är väl förankrade i exempel.
1. Analys är klart definierad av Pappus, och det är en användbar term som beskriver ett typiskt sätt att göra upp en plan genom att starta från det okända (eller slutsatsen) och arbeta baklänges mot det givna (eller antagandet). Olyckligtvis har ordet fått många olika betydelser (t.ex. i matematisk, kemisk, logisk analys) och har därför tyvärr måst undvikas i denna framställning.
2. Antagande betecknar en väsentlig del av en matematisk sats av det mera vanliga slaget (se Sökproblem, bevisproblem, 4). Termen är i denna mening helt klar och tillfredsställande. Svårigheten är att varje del av hypotesen också kallas för hypotes, så att hypotesen kanske består av ett antal hypoteser. Ett botemedel skulle kunna vara att kalla varje del av den fullständiga hypotesen för en "klausul" eller någonting liknande (se även punkt 9).
3. Huvuddelar i ett problem definieras i Sökproblem, bevisproblem, 3, 4.
4. Lösning är i sin rent matematiska betydelse en fullkomligt klar term. Den avser varje utsaga som satisfierar villkoret i ett "sökproblem". Så är t.ex. lösningen av ekvationen x² - 3x + 2 = 0 dess rötter, talen 1 och 2. Olyckligtvis har ordet också andra betydelser som inte är rent matematiska men som används av matematiker tillsammans med dess matematiska betydelse. Lösning kan också betyda "processen att lösa ett problem" eller "arbetet som lagts ned på att lösa problemet". Vi använder ordet i denna betydelse när vi talar om en "besvärlig lösning". Lösning kan också betyda resultatet av det arbete som lagts ned på att lösa problemet. Vi använder ordet i denna betydelse när vi talar om en "elegant lösning". Nu kan det hända att vi i samma mening måste tala om både den utsaga som satisfierar problemets villkor och om vägen för att finna den och om resultatet av arbetet. Om vi faller för frestelsen att kalla alla dessa tre saker för "lösning" kommer meningen att bli ganska oklar.
5. Progressiv argumentation har använts i skilda betydelser av olika författare och i den gamla betydelsen av "syntes" (se punkt 7) av några författare. Den senare användningen är försvarbar men termen har undvikits här.
6. Regressiv argumentation har använts i den äldre betydelsen av "analys" av några författare (jämför punkt 1 och 5). Termen är försvarbar men har undvikits här.
7. Syntes används av Pappus i en väldefinierad mening som skulle förtjäna att bevaras. Emellertid måste termen tyvärr undvikas i denna framställning av samma anledning som dess motsvarighet analys (se punkt 1).
8. Sökproblem, bevisproblem är ett par nya termer som tyvärr har måst introduceras för att ersätta historiska termer, vilkas betydelse emellertid har blivit hopplöst förvirrande i dagligt tal. I latinska versioner av grekisk matematisk text har båda dessa typer av problem den gemensamma benämningen "propositio". Ett "sökproblem" kallas "problema", ett "bevisproblem" "theorema". I gammaldags matematiskt språk har orden proposition (påstående), problem, teorem fortfarande sin euklidiska betydelse, men eftersom denna helt har ändrats i modernt matematiskt språkbruk är det berättigat att införa de nya termerna.
9. Villkor relaterar det sökta med det givna i ett "sökproblem" (se Sökproblem, bevisproblem, 3). I denna betydelse är det en klar, användbar och oumbärlig term. Emellertid är det ofta nödvändigt att dela upp villkoret i flera delar [i delarna a) och b) i exemplen Uppdelning och rekombinering, 7, 8]. Varje del av villkoret kallas då vanligen också för ett villkor. Denna tvetydighet som ibland är förvirrande skulle lätt kunna undvikas genom att man införde någon teknisk term för att beteckna de olika delarna av villkoret. En sådan del skulle t.ex. kunna kallas en "klausul" (se även punkt 2).
Betrakta den obekanta. Detta är ett gammalt råd. Motsvarande latinska fras är: "Respice finem", dvs. se på slutet. Kom ihåg avsikten. Glöm inte målet. Tänk på det som du vill uppnå. Förlora inte ur sikte det som efterfrågas. Håll i minnet vad du arbetar på. Betrakta den obekanta! Betrakta påståendet! De två sista versionerna av "respice finem" är speciellt lämpade för matematiska problem, för "sökproblem" resp. "bevisproblem".
Om vi inriktar vår uppmärksamhet på målet och koncentrerar vår beslutsamhet på föresatsen tänker vi på metoder och vägar att uppnå målet. Vad finns det för medel till förfogande? Hur kan man nå målet? Hur kan man komma fram till ett sådant resultat? Vilka orsaker skulle kunna ge ett sådant resultat? I vilket sammanhang har vi sett ett sådant resultat? Vad gör folk normalt för att komma fram till ett sådant resultat? Försök finna ett känt problem med samma eller liknande obekanta storhet. Försök finna en känd sats med samma eller liknande påstående. De två sista uppmaningarna är speciellt anpassade till "sökproblem" resp. "bevisproblem".
1. Vi skall betrakta matematiska problem, "sökproblem", och uppmaningen: Försök finna ett känt problem med samma obekanta storhet. Låt oss jämföra denna uppmaning med den som ligger i frågan Känner du till något närbesläktat problem?
Den sista meningen innebär en mer allmän uppmaning än den tidigare. Om ett problem är närbesläktat med ett annat har de två någonting gemensamt. De kan ha några gemensamma begrepp. De kan ha något givet eller någon del av villkoret gemensamt osv. Vår första uppmaning anger en särskild gemensam storhet: Problemen skall ha samma obekanta storhet. Den okända storheten skall alltså i båda fallen vara ett element tillhörande samma kategori, t.ex. längden av en rät linje.
Jämfört med den allmännare uppmaningen innebär den speciella en viss besparing i arbete.
Först och främst kan vi bespara oss besväret att föreställa oss problemet. Vi behöver inte genast se på hela problemet utan enbart på den obekanta storheten. Problemet framstår schematiskt såsom
"Om … beräkna längden av linjen."
Dessutom får vi det lättare när vi gör vårt val. Många problem kan vara besläktade med det givna problemet genom att ha en eller annan punkt gemensam med detta. Men om vi betraktar den obekanta storheten begränsar vi vårt val. Vi tar bara med sådana problem som har samma obekanta. Bland dessa problem betraktar vi självfallet först och främst dem som är mest elementära och som vi bäst känner till.
2. Det aktuella problemet har formen:
"Om … beräkna längden av linjen."
De enklaste och mest kända problemen av denna typ handlar om trianglar: Om tre element i en triangel är kända beräkna längden av en av sidorna. Kan vi dra oss detta till minnes har vi funnit någonting som mycket väl kan vara relevant: Här är ett närbesläktat problem som är löst förut. Skulle man kunna använda det? Skulle man kunna använda dess resultat? För att kunna använda det vi känner till om trianglar måste vi ha en triangel i vår figur. Finns det någon triangel där? Eller skall vi införa en för att sedan kunna dra fördel av dessa kända resultat? Skulle man kunna införa något hjälpelement så att man kan använda dessa?
Det finns åtskilliga enkla problem vars obekanta är sidan i en triangel. (De skiljer sig från varandra i vad som är givet. Två vinklar kan vara kända och en sida, eller två sidor och en vinkel, och läget av vinkeln i förhållande till de givna sidorna kan vara olika. Speciellt enkla är dessa problem för rätvinkliga trianglar.) Med uppmärksamheten riktad på det problem vi har framför oss försöker vi nu att finna vilken triangel vi bör införa, vilket tidigare löst problem (med samma obekanta som den vi har framför oss) som vore lämpligast att anpassa för vårt aktuella ändamål.
När vi har infört en lämplig hjälptriangel kan det hända att vi ännu inte känner de tre element som behövs för att bestämma triangeln. Detta är emellertid inte absolut nödvändigt. Om vi på förhand vet att det felande elementet kan erhållas på något sätt har vi gjort ett väsentligt framsteg. Vi har en plan för vår lösning.
3. Den procedur som är skisserad i avsnitt 1 och 2 illustreras i väsentliga drag genom avsnitt 10(illustrationen är något oklar beroende på elevernas tröghet). Det är inte alls svårt att finna åtskilliga liknande exempel. I själva verket kan lösningen av nästan alla de "sökproblem" som vanligtvis ges i mindre avancerade studier sättas i gång genom lämplig användning av uppmaningen: Försök finna ett känt problem med samma eller liknande obekanta storhet.
Vi skall behandla sådana problem schematiskt och tittar först på den obekanta storheten:
a) Om … beräkna längden av linjen.
b) Om … beräkna vinkeln.
c) Om … beräkna tetraederns volym.
d) Om … konstruera punkten.
Om vi har någon erfarenhet av att handskas med elementära matematiska problem kommer vi omedelbart att erinra oss diverse enkla och bekanta problem eller problem som har samma obekanta. Om det givna problemet inte tillhör dessa enkla bekanta problem försöker vi naturligtvis utnyttja det som är bekant för oss och dra fördel av resultatet av dessa enkla problem. Vi försöker införa något välkänt som kan vara användbart i problemet, och detta kan vara en god början.
I vart och ett av de fyra ovannämnda fallen finns en uppenbar plan, en rimlig gissning om hur lösningen kommer att se ut.
a) Den obekanta kan erhållas som en sida i någon triangel. Det återstår att införa en lämplig triangel med tre kända eller lättfunna element.
b) Den obekanta kan erhållas som en vinkel i någon triangel. Det återstår att införa någon lämplig triangel.
c) Den obekanta kan erhållas om höjden och ytan av basen är kända. Det återstår att finna ytan av en sida och den motsvarande höjden.
d) Den obekanta kan erhållas som skärningspunkten mellan två kurvor (geometriska orter) som vardera kan vara antingen en cirkel eller en rät linje. Det återstår att plocka fram sådana kurvor ur det givna villkoret.
I alla dessa fall antyds en plan genom ett enkelt problem med samma obekanta storhet och vars resultat eller metod vi vill utnyttja. Följer vi en sådan plan kan vi naturligtvis råka i svårigheter men vi har i alla fall en idé som vi kan börja med, vilket är en stor fördel.
4. Vi får ingen sådan fördel om det inte finns något tidigare löst problem med samma obekanta storhet som det givna problemet. I sådana fall är det mycket svårare att angripa det givna problemet.
"Beräkna ytan av en sfär med given radie." Detta problem löstes av Arkimedes. Det finns knappast något enklare problem med samma obekanta storhet och det fanns förvisso inget sådant enklare problem som Arkimedes skulle ha kunnat använda. Utan tvivel måste Arkimedes lösning betraktas som en av de märkligaste matematiska prestationerna.
"Beräkna ytan av en sfär som är inskriven i en tetraeder vilkens sex kanter är givna." Om vi känner till Arkimedes resultat, behöver vi inte hans geni för att lösa problemet. Vi behöver bara finna ett uttryck för sambandet mellan den inskrivna sfärens radie och tetraederns sex kanter. Detta är kanske inte alldeles lätt men svårigheten kan inte jämföras med den i Arkimedes problem.
Att känna till eller inte känna till ett tidigare löst problem med samma obekanta storhet kan vara hela skillnaden mellan ett lätt och ett svårt problem.
5. När Arkimedes beräknade ytan av en sfär kände han inte till något tidigare löst problem med samma obekanta storhet. Men han kände olika tidigare lösta problem som hade en liknande obekant storhet. Det finns krökta ytor som är lättare att beräkna än sfärens och som var välkända på Arkimedes tid. Dit hör t.ex. sidoytan av en rät cirkulär cylinder, av en rät cirkulär kon och av stympade cirkulära koner. Vi kan vara övertygade om att Arkimedes omsorgsfullt betraktade dessa enklare liknande fall. Han använde i själva verket i sin lösning som en approximation av sfären en sammansatt kropp bestående av två koner och ett antal stympade koner (se Definition, 6).
Om vi inte kan finna något tidigare löst problem med samma obekanta storhet som det aktuella problemet skall vi försöka finna ett med en liknande obekant storhet. Problem av det senare slaget är ju inte så närbesläktade med det aktuella problemet och kan därför vara svårare att använda än problem med samma obekanta storhet. Icke desto mindre kan de ofta ge värdefull ledning.
6. Vi lägger till några kommentarer beträffande "bevisproblem". De är analoga med de föregående mera utförliga kommentarerna till "sökproblem".
Vi skall bevisa (eller vederlägga) en klart formulerad sats. Varje sats som har bevisats tidigare och som på något sätt är besläktad med den aktuella satsen kan bli användbar, Omedelbar hjälp kan vi emellertid få av satser med samma påstående som den aktuella satsen. Därför bör vi betrakta påståendet, dvs. vi granskar vår sats och framhäver därvid påståendet. Vårt sätt att se på satsen kan då uttryckas schematiskt som:
"Om … så är vinklarna lika."
Vi koncentrerar oss på påståendet framför oss och försöker att finna en känd sats med samma eller liknande påstående. Framför allt försöker vi komma på några mycket enkla kända satser av detta slag.
I det här fallet finns det åtskilliga liknande satser, och vi kanske påminner oss följande: "Om två trianglar är kongruenta är motsvarande vinklar lika stora." Här är en närbesläktad sats som bevisats förut. Skulle man kunna använda den? Skulle man kunna införa något hjälpelement så att man kan använda den?
Om vi följer dessa uppmaningar och försöker bedöma den hjälp som erbjuds genom den sats vi kom på, kan vi göra upp en plan. Låt oss försöka bevisa att vinklarna i fråga i kongruenta trianglar är lika. Vi finner att vi måste införa ett par trianglar som innehåller dessa vinklar och visa att de är kongruenta. En sådan plan är säkerligen bra att börja med och kan slutligen leda till det önskade målet som i avsnitt 19.
7. Låt oss summera. Om vi kommer på tidigare lösta problem med samma eller liknande obekanta (tidigare bevisade satser med samma eller liknande påstående) finns det stora möjligheter att vi kommer i rätt riktning och vi kan göra en plan över hur vi skall komma fram till lösningen. I enkla fall, som är de vanligaste på elementära stadier, är som regel de mest elementära problemen med samma obekanta (satser med samma påstående) helt tillräckliga. Att försöka komma på problem med samma obekanta är en nästan självklar metod som bygger på sunt förnuft (jämför vad som sades i detta avseende i avsnitt 4). Det är ganska överraskande att en sådan enkel och användbar metod inte är mera känd än den är. Författaren är böjd att tro att den inte ens har formulerats förut i allmän betydelse. I vilket fall som helst bör varken elever eller lärare i matematik försumma att använda uppmaningen: Betrakta den obekanta! Försök finna ett känt problem med samma eller liknande obekanta storhet.
Bolzano, Bernhard (1781-1848), logiker och matematiker, ägnade en stor del av sin omfattande framställning av logiken, Wissenschaftslehre, åt ämnet heuristik (vol. 3, s. 293575). Han skriver om denna del av sitt arbete: "Jag tror inte alls att jag här kommer att beskriva någon undersökningsmetod som inte alla begåvade människor har kunnat beskriva för länge sedan. Jag kan inte alls lova att ni här skall finna någonting helt nytt. Men jag skall bemöda mig att i klara ord formulera de regler och undersökningsmetoder som alla begåvade personer använder, även om de i de flesta fall inte ens är medvetna om att de gör det. Fastän jag inte har några illusioner om att ens lyckas helt med detta, hoppas jag ändå att det lilla som presenteras här skall kunna intressera en del människor och kunna tillämpas senare."
Definition av ett begrepp är en förklaring av dess betydelse med hjälp av andra begrepp som antas vara väl kända.
1. Matematiska facktermer är av två slag. Några accepteras som enkla begrepp och definieras inte. Andra betraktas som härledda begrepp och definieras i vederbörlig ordning, dvs. deras betydelse förklaras med hjälp av enkla begrepp och tidigare definierade härledda begrepp. Sålunda ger vi t.ex. inte någon formell definition av sådana enkla begrepp som punkt, rät linje och plan.|2| Men vi ger formella definitioner av sådana begrepp som "en vinkels bisektris" eller "cirkel" eller "parabel"
Definitionen av parabel kan formuleras på följande sätt. Parabel kallar vi orten för punkter vilka ligger lika långt från en given punkt som från en given rät linje. Den givna punkten kallas parabelns brännpunkt, den givna linjen dess styrlinje. Det tas för givet att alla ingående element ligger i ett och samma plan och att den givna punkten (brännpunkten) inte ligger på den givna linjen (styrlinjen).
Läsaren antas inte känna till betydelsen av de definierade termerna: parabel, parabelns brännpunkt, parabelns styrlinje. Men han antas känna till betydelsen av alla andra använda begrepp såsom punkt, rät linje, plan, avståndet från en punkt till en annan punkt, (geometrisk) ort etc.
2. Definitioner i ordböcker skiljer sig inte mycket från matematiska definitioner vad beträffar den yttre formen, men de är skrivna i en annan anda.
Den som skriver en ordbok intresserar sig för ordens aktuella och allmänt godtagna betydelse. Han accepterar naturligtvis den gängse betydelsen och formulerar den så klart han kan i en definition.
Matematikern intresserar sig inte för den allmänna betydelsen av de facktermer han använder. Åtminstone är han inte primärt intresserad av den. Vad "cirkel" eller "parabel" eller andra facktermer av liknande slag än må betyda i dagligt tal spelar liten roll för honom. Den matematiska definitionen skapar den matematiska betydelsen.
3. Exempel. Konstruera skärningspunkten mellan en given rät linje och en parabel för vilken brännpunkten och styrlinjen är kända.
Vårt sätt att attackera ett problem måste bero på vår kunskapsnivå. Hur vi angriper föreliggande problem beror huvudsakligen på vad vi känner till om parabelns egenskaper. Om vi vet en hel del om parabeln försöker vi använda våra kunskaper och plocka ut något som är relevant i sammanhanget: Känner du till någon sats som skulle kunna användas? Känner du till något närbesläktat problem? Om vi däremot vet bara något om parabel, brännpunkt och styrlinje är dessa begrepp snarast förvirrande och det är naturligt om vi vill bli av med dem. Hur kan vi bli av med dem? Låt oss lyssna till dialogen mellan den lärare och elev som diskuterar det givna problemet. De har redan valt lämpliga beteckningar: P för någon av de okända skärningspunkterna, B för brännpunkten, s för styrlinjen, c för den räta linjen som skär parabeln.
"Vad är det som söks?"
"Punkten P."
"Vad är det som är givet?"
"De räta linjerna c och s och punkten B."
"Hur lyder villkoret?"
"P är skärningspunkten mellan den räta linjen c och parabeln, som har styrlinjen s och brännpunkten B."
"Riktigt. Jag vet att du inte har lärt dig så mycket om parabler, men jag tror du kan säga vad en parabel är."
"Parabeln är geometriska orten för punkter som ligger lika långt från brännpunkten som från styrlinjen."
"Bra! Du kommer ihåg definitionen helt korrekt. Men vi måste också kunna använda den. Gå tillbaka till definitionerna. Vad skulle du kunna säga om punkten P med utgångspunkt från parabelns definition?
"P ligger på parabeln. Därför ligger P lika långt från s som från B."
| Fig 16. |  |
"Bra! Rita en figur."
Eleven ritar nu in linjen PB och PQ. Den senare är normalen från P till s.
"Skulle du kunna formulera om problemet?"
…
"Skulle du kunna formulera om problemets villkor genom att använda de linjer du nu fört in?"
"P är en punkt på linjen c så att PB = PQ."
"Bra. Men säg detta i ord: Vad är PQ?"
"Vinkelräta avståndet från P till s."
"Bra. Skulle du kunna formulera om problemet nu? Men försök formulera det i en fullständig och klar mening."
"Konstruera på den givna räta linjen c en punkt P som ligger lika långt från en given punkt B och en given rät linje s."
"Lägg märke till det framsteg som gjorts från den ursprungliga formuleringen till din nya formulering. Den ursprungliga formuleringen av problemet var full med obekanta facktermer såsom parabel, brännpunkt, styrlinje. Den lät något pompös. Nu återstår ingenting av dessa obekanta facktermer. Du har stuckit hål på ballongen. Bra gjort!"
4. Eliminering av facktermer är resultatet av vårt arbete i föregående exempel. Vi utgick från en formulering av problemet som innehöll vissa tekniska termer (parabel, brännpunkt, styrlinje) men kunde till slut ge det en ny formulering utan dessa termer.
För att kunna eliminera en fackterm måste vi veta dess definition. Men detta räcker inte, vi måste använda definitionen också. I ovanstående exempel var det inte tillräckligt att komma ihåg hur en parabel definierades. Det avgörande var att i vår figur föra in linjerna PB och PQ som enligt parabelns definition är lika långa. Detta är en typisk procedur. Vi för in lämpliga element i problemet. Vi ställer upp relationer mellan dessa element, baserade på definitionen. Om dessa relationer uttrycker betydelsen på ett fullständigt sätt har vi använt definitionen. I och med att vi använt facktermens definition har vi också eliminerat facktermen.
Den process vi just beskrivit kan kallas att gå tillbaka till definitionerna. Genom att gå tillbaka till definitionen av en fackterm kan vi bli av med termen men inför i stället nya element och motsvarande nya relationer. Den ändring i vår uppfattning av problemet som blir följden kan vara betydande. Hur som helst måste någon omformulering, någon variation av problemet ge resultat.
5. Definitioner och kända satser. Om vi känner till ordet "parabel" och har någon vag idé om kurvans form men för övrigt inte vet någonting om den, är våra kunskaper uppenbarligen otillräckliga för att lösa problemet ovan eller för att lösa något annat seriöst geometriskt problem rörande en parabel. Vad är det vi då behöver kunna?
Geometrin kan anses bestå av axiom, definitioner och satser. Parabeln nämns inte i axiomen, vilka enbart handlar om sådana enkla begrepp som punkt, rät linje osv. Ett geometriskt resonemang som handlar om en parabel eller lösningen av något problem där den är inblandad, måste antingen använda definitionen av parabeln eller satser som handlar om den. För att lösa ett sådant problem måste vi åtminstone kunna definitionen, men ännu bättre är det att dessutom känna till några satser.
Vad vi här sagt om parabeln gäller naturligtvis om alla härledda begrepp. När vi börjar lösa ett problem som innehåller ett sådant begrepp, vet vi till en början inte vad som kommer att vara fördelaktigast att använda, definitionen av begreppet eller någon sats om detta. Men vi måste med säkerhet använda endera av dem.
Det finns emellertid fall där vi inte har något val. Om vi endast känner till begreppets definition och ingenting annat är vi tvungna att använda denna. Om vi inte kan mycket mer än definitionen är det förmodligen bäst att gå tillbaka till denna. Men om vi känner till flera satser som handlar om begreppet i fråga och om vi har längre erfarenhet av dem kanske vi kan komma på någon lämplig sats i stället.
6. Flera definitioner. En sfär definieras vanligen som orten för punkter som alla ligger på ett givet avstånd från en given punkt. (Punkterna ligger nu i rummet och är inte begränsade till ett plan.) Men sfären skulle också kunna definieras som den yta en cirkel beskriver när den roterar kring en diameter. Flera andra definitioner av sfären är välkända, och många andra är möjliga.
När vi skall lösa ett problem som handlar om något härlett begrepp, t.ex. "sfär" eller "parabel", har vi flera möjligheter att välja mellan om vi vill gå tillbaka till definitionen. Mycket kan i ett sådant fall bero på om vi väljer den definition som passar problemet bäst.
Att beräkna sfärens yta var, när Arkimedes löste det, ett stort och svårt problem. Arkimedes kunde välja mellan de två definitioner av sfären som vi just redogjorde för. Han föredrog att uppfatta sfären som den yta som alstras av en cirkel som roterar kring en given diameter. Han inskriver denna cirkel i en regelbunden månghörning med ett jämnt antal sidor och i vilken två motstående hörn förbinds genom cirkelns diameter. Den reguljära polygonen approximerar cirkeln, och när den roterar med denna alstrar den en konvex yta sammansatt av två koner med sina spetsar i diameterns ändpunkter och ett antal stympade koner däremellan. Denna sammansatta yta approximerar sfären och användes av Arkimedes när han beräknade sfärens yta. Om vi däremot föreställer oss sfären som orten för alla punkter som ligger lika långt från centrum, så får vi ingen antydan om någon liknande enkel approximation.
7. Att gå tillbaka till definitionerna kan vara av betydelse för att komma på ett argument men också för att kontrollera det.
Någon hävdar att han har funnit en ny lösning till Arkimedes problem att finna sfärens yta. Om han bara har en vag idé om sfären kan hans lösning inte vara bra. Han må ha en klar föreställning av sfären men om han inte använder den i sin argumentation kan man ju inte veta om han hade någon föreställning alls, och hans resonemang kan inte övertyga. Om jag därför lyssnar på hans argumentation väntar jag på det ögonblick där han skall säga någonting väsentligt om sfären, använda definitionen av den eller någon sats som handlar om den. Om ett sådant ögonblick aldrig kommer är lösningen dålig.
Vi skall inte bara kontrollera andras argument utan naturligtvis även våra egna på samma sätt. Har du tagit hänsyn till alla nödvändiga begrepp som ingår i problemet? Hur använde du dessa begrepp? Använde du deras betydelse, deras definition? Använde du några väsentliga fakta, några kända satser om dessa begrepp?
Att det var värdefullt att gå tillbaka till definitionerna när man kontrollerar giltigheten av ett resonemang underströks av Pascal som formulerade regeln: "Substituez mentalement les définitions ā la place des définis." (Byt ut i tankarna de definierade storheterna mot deras definitioner.) Betydelsen av att gå tillbaka till definitionerna när man vill konstruera ett bevis har understrukits av Hadamard.
8. Att gå tillbaka till definitionerna är en betydelsefull tankeoperation. Om vi vill förstå varför definitioner av ord är så viktiga måste vi först inse att ord är viktiga. Vi kan knappast tänka utan att använda ord eller tecken eller något slag av symboler. Ord och tecken har följaktligen makt. Primitiva folkslag tror att ord och symboler har magisk kraft. Vi kan förstå en sådan tro men vi bör inte dela den. Vi måste inse att kraften i ett ord inte ligger i dess klang, i dess "vocis flatus", i den luftström som talaren frambringar, utan i de föreställningar ordet påminner oss om och slutligen i de fakta som dessa föreställningar bygger på.
Därför är det en sund strävan att söka betydelser och fakta bakom orden. När matematikern går tillbaka till definitionerna försöker han få ett begrepp om de verkliga relationerna mellan matematiska objekt, som kan finnas dolda i facktermerna, precis som fysikern vill se bestämda experimentella fakta bakom sina facktermer, och mannen på gatan som har sunt förnuft hellre vill finna kalla realiteter än låta sig föras bakom ljuset av blotta ord och fraser.
Dela upp villkorets olika delar. Vår första skyldighet är att förstå problemet. När vi har förstått det i sin helhet går vi in på detaljerna. Vi tittar på huvuddelarna, det som söks, det som är givet, villkoret, var och en del för sig. När dessa delar står klara för oss men vi fortfarande inte har någon speciellt användbar idé, går vi djupare in i detaljerna. Vi betraktar de givna storheterna var och en för sig. När vi har förstått villkoret i sin helhet delar vi upp dess olika delar och tittar på var del för sig.
Nu ser vi vilken roll denna uppmaning spelar. Den försöker få oss att ta ett steg som vi måste ta när vi försöker se problemet klart och måste gå djupare in i detaljerna. Det är ett steg som ingår i processen Uppdelning och rekombinering.
Dela upp villkorets olika delar. Kan du skriva ner dem? Vi har ofta anledning att ställa denna fråga när vi arbetar med Att ställa upp ekvationer.
Den blivande matematikern bör vara en god problemlösare. Men det räcker inte. I sinom tid kommer han att lösa betydelsefulla matematiska problem men först bör han komma underfund med vilket slags problem hans naturliga begåvning bäst lämpar sig för.
Det viktigaste för honom är att se tillbaka på varje fullbordad lösning. Genom att gå igenom arbetet och undersöka den slutliga lösningens form kan han finna en obegränsad rikedom av detaljer att granska. Han kan fundera över svårigheten med problemet och över den avgörande idén. Han kan försöka lista ut vad det var som hindrade honom och vad som slutligen hjälpte honom. Han kan hålla utkik efter enkla intuitiva idéer: Kan dit se det direkt? Han kan jämföra och utveckla olika metoder: Kan du härleda resultatet på något annat sätt? Han kan försöka att klargöra problemet genom att jämföra det med problem som lösts förut. Han kan försöka konstruera nya problem som han kan lösa med hjälp av det just avslutade arbetet: Kan du använda resultatet eller metoden för något annat problem? Genom att tänka över de problem han löst så fullständigt som möjligt kan han förvärva välordnade kunskaper som är färdiga att användas.
Den blivande matematikern lär sig, precis som alla andra, genom att härma och genom att öva. Han bör se till att han tar efter den riktiga modellen. Han bör observera en stimulerande lärare. Han bör tävla med en duktig kamrat. Sedan måste han, vilket förmodligen är det viktigaste av allt, läsa inte bara de gängse läroböckerna utan goda författare i allmänhet tills han finner någon, vars stil och metod är sådana att han har lätt att härma dem. Han måste uppskatta och leta efter det som han tycker verkar enkelt eller lärorikt eller vackert. Han måste lösa problem, välja de problem som passar honom, begrunda deras lösning och konstruera nya problem. Med dessa och med alla andra medel bör han sträva efter att göra sin första stora upptäckt: han måste upptäcka vad han tycker om och inte tycker om, han måste upptäcka sin smak och sin egen profil.
Den intelligente läsaren av en matematisk bok önskar två saker:
För det första att se att det aktuella steget i argumentationen är korrekt.
För det andra att inse syftet med det aktuella steget.
Den intelligente åhöraren har samma önskemål under en matematisk föreläsning. Om han inte kan inse att det aktuella steget i argumentationen är korrekt eller t.o.m. misstänker att det möjligen är felaktigt, kanske han protesterar och ställer en fråga. Om han inte kan se någon mening i det aktuella steget eller ana något skäl för det, så kan han vanligen inte ens formulera en klar invändning. Han protesterar inte, han blir enbart förskräckt och uttråkad och förlorar den röda tråden i argumentationen.
Den intelligente läraren och den intelligente läroboksförfattaren bör tänka på detta. Att skriva och tala korrekt är naturligtvis nödvändigt, men det är inte tillräckligt. En härledning som presenteras korrekt i en bok eller vid svarta tavlan kan vara otillgänglig och ointressant om avsikten med de sammanhängande stegen är obegriplig, om läsaren eller åhöraren inte kan förstå hur en mänsklig hjärna kan komma fram till ett sådant argument, om han inte ur framställningen kan finna en antydan om hur han själv skulle kunna komma på ett sådant argument.
Frågorna och uppmaningarna i vår lista kan kanske hjälpa författaren eller läraren att understryka syftet och motivet med sina argument. Speciellt användbar i detta avseende är frågan: Använde vi alla de givna uppgifterna? Med denna fråga kan författaren eller läraren ge ett gott skäl för att granska en uppgift som ännu inte har använts. Läsaren eller åhöraren kan använda samma fråga för att förstå författarens eller lärarens skäl att granska den ena eller den andra detaljen, och han kanske finner att om han bara hade ställt denna fråga så skulle han själv ha förstått steget i argumentationen.
Den intelligente problemlösaren ställer sig ofta frågor liknande dem i vår lista. Han kanske själv har kommit på frågor av detta slag eller upptäckt deras användbarhet sedan han hört en sådan fråga någon gång. Förmodligen är han inte alls medveten om att han upprepar samma stereotypa fråga om och om igen. Kanske är frågan en av hans speciella favoriter. Han vet att den är en del av hans tankemönster, lämplig under en viss fas av arbetet, och han frammanar den rätta tankebanan genom att ställa den rätta frågan.
Den intelligente problemlösaren kanske finner frågorna och uppmaningarna på vår lista användbara. Han kanske väl förstår de förklaringar och exempel som illustrerar en viss fråga, han kanske inser hur frågan bör användas. Men han kan inte komma fram till verklig insikt såvida han inte kommer på det förfaringssätt som frågan försöker framkalla i hans eget arbete och upptäcker hur han själv skulle kunna använda frågan.
Den intelligente problemlösaren skall vara beredd att ställa alla frågorna på listan, men han bör inte använda någon av dem såvida han inte manas att göra det av sitt eget opartiska omdöme när han omsorgsfullt tänker igenom problemet. Han måste naturligtvis avgöra själv om den givna situationen är eller inte är tillräckligt lik någon annan situation i vilken frågan har använts med framgång.
Den intelligente problemlösaren försöker först av allt att förstå problemet så fullständigt och så klart som möjligt. Men att enbart förstå räcker inte. Han måste koncentrera sig på problemet, han måste allvarligt önska att komma fram till dess lösning. Om han inte kan mobilisera en verklig önskan att lösa problemet vore det bättre om han lämnade det därhän. Hemligheten bakom verklig framgång ligger i att kasta sig in i problemet med hela sin själ.
Den traditionelle matematikprofessorn, som hör hemma i anekdoterna, är tankspridd. Vanligen glömmer han sitt paraply var han går. Han föredrar att vända näsan mot svarta tavlan och ryggen mot auditoriet. Han skriver A, säger B och menar C, när det skall vara D. En del av hans visdomsord överförs från generation till generation.
"För att lösa denna differentialekvation betraktar man den tills lösningen uppenbarar sig."
"Denna princip är så fullkomligt allmän att det inte är möjligt att tillämpa den i något speciellt fall."
"Geometri är konsten att argumentera korrekt om felaktiga figurer."
"Min metod att övervinna en svårighet är att undvika den."
"Vad är det för skillnad mellan en metod och ett knep? En metod är ett knep som man använder två gånger."
När allt kommer omkring kan man lära sig åtskilligt av denne traditionelle matematikprofessor. Låt oss hoppas att den matematiklärare som du inte lär dig någonting av inte kommer att bli traditionell.
Descartes, René (1596 — 1650), matematiker och filosof, hade planer på att utforma en universell metod att lösa problem, men han fullbordade aldrig sitt verk Regler för tankens vägledning. Fragment av detta arbete, som återfanns i manuskript och trycktes efter hans död, innehåller mer — och mer intressant — material som behandlar problemlösning än hans bättre kända verk Discours de la Méthode, fastän detta sannolikt skrevs senare. Följande rader av Descartes verkar beskriva upphovet till hans "Regler": "När jag som ung man hörde talas om geniala uppfinningar försökte jag att uppfinna dem själv, t.o.m. utan att läsa författaren. När jag gjorde detta märkte jag så småningom att jag använde vissa regler."
Det undermedvetna arbetet. En afton ville jag diskutera en viss författare med en vän men jag kunde inte komma ihåg författarens namn. Jag blev förargad för jag kom ganska väl ihåg en av hans historier. Jag erinrade mig också någon historia om författaren själv som jag ville berätta. I själva verket kom jag ihåg allting utom hans namn. Gång efter annan försökte jag förgäves att påminna mig detta namn. Så snart jag följande morgon tänkte på min irritation från kvällen förut kom jag på namnet utan minsta ansträngning.
Det är troligt att läsaren själv har gjort någon liknande erfarenhet. Om han är en hängiven problemlösare har han förmodligen haft någon liknande erfarenhet med ett problem. Det förekommer ofta att man inte har någon framgång alls med ett problem. Man arbetar mycket hårt men kommer ändå ingen vart. Men när man återvänder till problemet efter en natts vila eller några dagars avbrott får man en snilleblixt och man löser problemet lätt. Problemets art betyder föga. Ett glömt ord, ett svårt ord i ett korsord, början på ett plågsamt brev eller lösningen till ett matematiskt problem kan dyka upp på detta sätt.
Sådana händelser ger intryck av undermedvetet arbete. Faktum är att ett problem efter att ha varit ur tankarna en tid kan återvända till medvetandet väsentligt klarare, mycket närmare sin lösning än det var när det försvann ur medvetandet. Vem redde ut det, vem förde det närmare lösningen? Uppenbarligen man själv, på ett undermedvetet sätt. Det är svårt att ge något annat svar, fastän psykologerna har upptäckt början till vad som en vacker dag kan visa sig vara ett mer tillfredsställande svar.
Vad teorin om det undermedvetna arbetet än må innehålla av värde är det säkert att det finns en gräns bortom vilken vi inte bör pressa det medvetna tänkandet. Det finns vissa tillfällen då det är bättre att lämna problemet en tid. "Sov på saken" är ett gammalt gott råd. Om vi låter oss själva och problemet vila kanske vi åstadkommer mer i morgon med mindre ansträngning. Men det är viktigt att inte lägga undan ett problem som vi önskar komma tillbaka till senare utan att ha intrycket av att ha kommit någon vart. Åtminstone bör någon liten detalj vara avklarad, någon aspekt av frågan belyst innan vi slutar arbetet.
Endast sådana problem återvänder förbättrade, vilkas lösning vi verkligen önskar eller som vi har arbetat verkligt hårt med. Medveten ansträngning tycks vara nödvändig för att sätta i gång det undermedvetna arbetet. Under alla förhållanden skulle det vara för lätt om det inte vore så. Vi skulle kunna lösa svåra problem bara genom att lägga oss att sova och vänta på en ljus idé.
I äldre tider betraktades en plötslig god ide som en inspiration, en gåva från gudarna. Vi måste förtjäna en sådan gåva genom arbete eller åtminstone genom en brinnande önskan.|3|
Diagnos används här som pedagogisk fackterm med betydelsen "närmare karakterisering av elevens arbete". Ett betyg karakteriserar en elevs arbete endast på ett grovt sätt. Den lärare som önskar förbättra elevens arbete behöver en bättre bestämning av goda och dåliga punkter precis som läkaren som vill förbättra patientens hälsa behöver en diagnos.
Vi är här speciellt intresserade av elevens förmåga att lösa problem. Hur kan vi fälla ett omdöme om den? Vi kan dra nytta av att särskilja de fyra faserna av lösningen. Elevernas beteende i dessa skilda faser är faktiskt mycket karakteristiskt.
Ofullständig insikt i problemet beroende på brist på koncentration är kanske den vanligaste bristen när det gäller att lösa problem. När det gäller förmågan att lägga upp en plan och få en allmän uppfattning om lösningen förekommer ofta två fel av motsatt slag. En del elever störtar sig direkt på beräkningar och konstruktioner utan någon som helst plan eller allmän idé. Andra väntar klumpigt att någon idé skall uppenbara sig och kan inte göra någonting som skulle kunna påskynda den. När det gäller att genomföra planen är slarv och otålighet det vanligaste felet. Eleven har inte den noggrannhet och det tålamod som fordras för att kontrollera varje steg. Uraktlåtenhet att kontrollera resultatet är också mycket vanlig. Eleven är glad att få ett svar över huvud taget, lägger ifrån sig pennan och är inte det minsta oroad av de mest osannolika resultat.
Den lärare som har gjort en noggrann diagnos på fel av detta slag har möjlighet att bota dem genom att ständigt upprepa och framhäva vissa frågor på listan.
Dimensionstest är en välkänd, snabb och effektiv metod att kontrollera geometriska eller fysikaliska formler.
1. För att friska upp minnet av hur metoden fungerar betraktar vi en stympad rät cirkulär kon. Låt R vara den undre radien, r den övre radien, h höjden och S storleken av den koniska sidoytan. Om R, r och h är givna, kan S uppenbarligen bestämmas. Vi finner uttrycket S = π(R + r) √[(R - r)² + h²], på vilket vi nu vill tillämpa ett dimensionstest.
Dimensionen av en geometrisk storhet framgår klart. Då R, r och h är längder mäts de i meter om vi använder vetenskapliga enheter, och deras dimension är m. Ytan S mäts i kvadratmeter, dess dimension är m². π = 3,14159… är bara ett tal. Om vi vill tillskriva en rent numerisk storhet en dimension måste den bli mº = 1.
Varje term i en summa måste ha samma dimension som summan själv. Så har R, r och R + r samma dimension, nämligen m. De två termerna (R - r)² och h² har samma dimension (som de måste ha), m².
En produkts dimension är lika med produkten av faktorernas dimensioner och en liknande regel gäller om potenser. Om vi ersätter storheterna med deras dimensioner på båda sidor om likhetstecknet i den formel vi vill testa får vi m² = 1 · m√m². Eftersom detta uppenbarligen är riktigt kunde testet inte avslöja något fel i formeln. Formeln klarade testet.
Andra exempel ges i avsnitt 14 och i Kan du kontrollera resultatet?, 2.
2. Vi kan tillämpa dimensionstestet på slutresultatet i ett problem eller på mellanresultat, på vårt eget arbete eller på andras arbete (mycket lämpligt för att söka fel i tentamensskrivningar), och även på formler som vi erinrar oss och på formler som vi gissar.
Om man påminner sig formlerna 4πr² och 4πr³/3 för ytan och volymen av en sfär men inte är alldeles säker på vilken som är vilken, så avslöjar dimensionstestet omedelbart hur det förhåller sig.
3. Dimensionstest är ännu viktigare inom fysiken än inom geometrin.
Låt oss betrakta en vanlig pendel, dvs. en liten tung kropp upphängd i en tråd vars massa vi kan försumma och vars längd vi betraktar som konstant. l betecknar trådens längd, g tyngdaccelerationen och T pendelns svängningstid.
En fysikalisk betraktelse visar nu att T enbart beror på l och g. Men vilken form har beroendet? Vi kanske påminner oss eller gissar att T = c · l a· g b, där c, a, b är vissa numeriska konstanter. Vi antar alltså att T är proportionell mot vissa potenser, l a, g b, av l och g.|4|
Titta nu på dimensionerna) T är en tid och mäts i sekunder, dess dimension är s. Dimensionen av längden l är m, dimensionen av accelerationen g är m·s-2 och dimensionen av den numeriska konstanten c är 1. Dimensionstestet ger oss nu ekvationen s = 1·ma·(m·s-2)b eller s = ma+b·s-2b. Eftersom vi måste ha samma potenser av grundenheterna m och s i båda leden i ekvationen får vi 0 = a + b och l = - 2b. Detta ger a = 1/2 och b = -1/2. Alltså måste uttrycket för svängningstiden T ha, formen T = c1½g½ = c√(l/g).
Dimensionstestet ger i detta fall åtskilligt men det kan inte ge allt. För det första kan det inte ge någon upplysning om värdet av konstanten c (som i själva verket är 2π). För det andra ger det ingen upplysning om att formelns giltighet är begränsad, Formeln gäller bara för små svängningar hos pendeln och endast approximativt. (Den är exakt för "oändligt små" svängningar.) Trots dessa begränsningar råder det inget tvivel om att dimensionsbetraktelsen har tillåtit oss att snabbt och med de mest elementära medel förutse en väsentlig del av ett resultat, vars utförliga härledning skulle fordra mycket mer avancerade metoder. Och så är det i många liknande fall.
Figurer är inte bara objektet i geometriska problem utan också en betydelsefull hjälp vid alla slags problem i vilka det inte finns någonting geometriskt till att börja med. Det finns alltså två skäl att titta på den roll som figurer spelar vid lösningen av problem.
1. Om ett problem är ett geometriskt problem måste vi arbeta med figur. Figuren kan finnas i vår fantasi eller också kan den ritas på ett papper. I vissa fall kan det vara värt att föreställa sig figuren utan att rita den, men om vi måste undersöka skilda detaljer, den ena efter den andra, är det bäst att rita en figur. Finns det många detaljer kan vi inte föreställa oss dem alla på en gång men de finns alla med på ett papper. En detalj som vi enbart föreställer oss kan vi glömma, men detaljen på papperet finns kvar där, och när vi kommer tillbaka till den påminner den oss om en tidigare iakttagelse. Den sparar oss besväret att komma ihåg vad vi tidigare har tänkt.
2. Vi ser nu mer speciellt på användningen av figurer i problem med geometriska konstruktioner.
Vi börjar bearbeta ett sådant problem i och med att vi ritar en figur som innehåller det som söks och det som är givet och som byggs upp av dessa element i enlighet med problemets villkor. För att kunna förstå problemet tydligt måste vi tänka över varje given storhet och varje del av villkoret för sig. Sedan lägger vi ihop delarna igen och betraktar villkoret som en helhet, samtidigt som vi försöker se de olika samband som ingår i problemet. Vi skulle knappast kunna handskas med alla dessa detaljer utan att ha en figur på ett papper.
Å andra sidan kan det vara tveksamt om en sådan figur alls kan ritas innan vi har löst problemet slutgiltigt. Är det möjligt att tillfredsställa hela det villkor som ställs i problemet? Vi har ingen möjlighet att säga ja innan vi har nått fram till den definitiva lösningen. Trots detta börjar vi med att förutsätta en figur i vilken det okända är relaterat med det givna på ett sätt som är föreskrivet av villkoret. Det verkar som om vi har gjort ett oberättigat antagande i och med att vi har ritat figuren.
Nej, det har vi inte. Inte nödvändigtvis. Vi gör inte fel när vi i vår undersökning av problemet antar möjligheten att det finns ett element som uppfyller det villkor som satts för det som söks och som har de föreskrivna relationerna med det givna, förutsatt att vi inte förväxlar möjlighet med säkerhet. En domare handlar inte fel när han under sin utfrågning antar som hypotes att svaranden har förövat brottet i fråga, såvida han inte binder sig vid denna hypotes. Både matematikern och domaren kan mycket väl opartiskt undersöka möjligheten men spara sitt omdöme tills undersökningen ger något definitivt resultat.
Metoden att börja undersökningen av ett konstruktionsproblem med att rita en skiss i vilken villkoret antas vara uppfyllt går tillbaka till grekiska geometriker. Den antyds av den korta, något gåtfulla frasen av Pappus: Antag att det som erfordras redan har utförts. Följande rekommendation är något mindre koncis men klarare: Rita en hypotetisk figur som antar problemets villkor uppfyllt i alla dess delar.
Detta är en rekommendation för problem i geometrisk konstruktion men i själva verket finns det ingen anledning att begränsa oss till sådana slags problem. Vi kan utvidga rekommendationen till alla "sökproblem" genom att formulera den på följande allmänna sätt: Undersök den hypotetiska situation i vilken problemets villkor antas vara fullständigt uppfyllt.
Jämför Pappus, 6.
3. Låt oss nu uppehålla oss vid några punkter rörande själva ritandet av figurerna.
a) Skall vi rita figurerna exakt eller approximativt, med hjälpmedel eller på fri hand?
Båda dessa alternativ har sina fördelar. Exakta figurer spelar i princip samma roll i geometrin som exakta mätningar i fysiken. Men i praktiken är exakta figurer mindre viktiga än exakta mätningar eftersom geometrins satser är verifierade i en helt annan utsträckning än fysikens lagar. Emellertid bör nybörjaren konstruera figurer så exakt som möjligt för att på detta sätt förvärva en god experimentell bas. Exakta figurer kan också ge den erfarne antydningar om geometriska satser. För argumentationens behov är emellertid figurer som dras omsorgsfullt på fri hand vanligen tillräckligt bra och de går mycket fortare att rita. Naturligtvis får figuren inte se omöjlig ut. Linjer som skall vara räta får inte gå i vågor och cirklar får inte se ut som potatisar.
En oriktig figur kan under vissa omständigheter framkalla en falsk slutsats men risken är inte stor. Vi kan skydda oss mot den på olika sätt, t.ex. genom att variera figuren. Det är ingen risk om vi koncentrerar oss på de logiska sammanhangen och tänker på att figuren är en hjälp och absolut inte grunden för våra slutsatser. De logiska sambanden utgör den verkliga basen. [Detta illustreras lärorikt av olika välkända paradoxer som på ett skickligt sätt utnyttjar en avsiktligt felaktig figur.]
b) Det är viktigt att figurens beståndsdelar har de föreskrivna relationerna men det är inte så noga i vilken ordning de konstrueras. Antag exempelvis att man vill illustrera vinkelns tredelning och önskar dra två vinklar, α och β, så att α = 3β. Om man börjar med en godtycklig vinkel α kan man aldrig konstruera β med passare och linjal. Därför väljer man en ganska liten men i övrigt godtycklig vinkel β, och från den konstruerar man α, vilket är lätt.
c) Figuren bör inte antyda något specialfall som inte är avsett. De skilda delarna av figuren bör inte uppvisa tydliga relationer som inte krävs av problemet. Linjer skall inte se ut att vara lika stora eller vinkelräta mot varandra, om de inte nödvändigtvis måste vara det. Trianglar skall inte se ut att vara likbenta eller rätvinkliga om ingen sådan egenskap ligger i problemet. Triangeln med vinklarna 45º, 60º, 75º är den som i bokstavlig mening befinner sig längst från både likbent och rätvinklig form.|5| Man kan rita en sådan eller en liknande triangel om man vill betrakta en "allmän" triangel.
d) För att framhäva de olika roller som olika linjer spelar, kan man rita tunna och tjocka linjer, heldragna eller streckade eller av olika färg. Man drar en linje mycket svagt om man ännu inte har beslutat att använda den som en hjälplinje. Man kan dra de givna elementen med rödpenna och använda andra färger för att framhäva viktiga delar, såsom ett par likformiga trianglar etc.
e) Bör man använda tredimensionella modeller för att illustrera rymdgeometri eller figurer på papper och svarta tavlan?
Tredimensionella modeller är mycket användbara men dyra och besvärliga att göra. Därför måste vi vanligtvis nöja oss med figurer fastän det inte är lätt att göra dem tydliga. Experimenterande med egenhändigt gjorda pappmodeller är mycket lämpligt för nybörjare. Att välja ett föremål från vårt dagliga liv för att representera geometriska begrepp underlättar en hel del. Så kan t.ex. en låda, en tegelsten eller klassrummet representera en rätvinklig parallellepiped, en penna en cirkulär cylinder, en lampskärm en stympad rät kon etc.
4. Figurer på papper är lätta att rita, lätta att känna igen, lätta att komma ihåg. Eftersom vi är speciellt förtrogna med plana figurer tycker vi också att problem som rör plana figurer är lätta. Vi kan dra nytta av denna omständighet. Vi kan använda vår förmåga att handskas med figurer till att behandla icke-geometriska objekt om vi kan tänka ut en lämplig geometrisk bild för dessa icke-geometriska objekt.
I själva verket används geometriska bilder, kurvor och diagram av alla slag i alla vetenskaper, inte bara i fysik, kemi och andra naturvetenskaper utan också i ekonomi och t.o.m. inom psykologi. Genom en lämplig geometrisk framställning kan vi försöka uttrycka allting i figurspråk och reducera alla slags problem till geometriska problem.
Även om ditt problem inte är geometriskt, skall du därför försöka rita en figur. Att hitta en klar och överskådlig geometrisk bild av ett icke-geometriskt problem kan betyda ett avgörande steg mot lösningen.
Framsteg och prestation. Har du gjort något framsteg? Vari låg den väsentliga prestationen? Vi kan ställa frågor av detta slag till oss själva när vi löser problem eller till en elev vars arbete vi övervakar. På så sätt blir vi vana vid att mer eller mindre tillförlitligt bedöma framsteg och prestation i konkreta fall. Steget från sådana konkreta fall till en allmän beskrivning är inte alls lätt. Ändå måste vi ta detta steg om vi vill göra vår undersökning av heuristiken något så när fullständig, och vi måste försöka reda ut vad framsteg och prestation i allmänhet innebär när det gäller problemlösning.
1. För att kunna lösa ett problem måste vi känna till något om ämnesområdet och vi måste samla upp och välja ut relevanta detaljer från våra befintliga men till en början slumrande kunskaper. Vår föreställning av problemet är mycket mera innehållsrik när vi har avslutat det än när vi började med det. Vad är det som har tillkommit? Det som vi lyckats plocka fram ur vårt minne. För att kunna prestera en lösning måste vi erinra oss diverse väsentliga fakta. Om vårt problem är matematiskt måste vi komma på tidigare lösta problem, kända satser och definitioner. Att dra fram sådana relevanta delar från vårt minne skulle kunna kallas mobilisering.
2. För att lösa ett problem är det emellertid inte tillräckligt att erinra sig isolerade fakta. Vi måste kombinera dessa fakta och denna kombination måste vara väl anpassad för problemet i fråga. Om vi löser ett matematiskt problem måste vi därför bygga upp ett argument som skapar samband och bringar reda i det material vi har samlat ihop. Denna anpassande och kombinerande aktivitet skulle kunna kallas organisering.
3. Mobilisering och organisering kan i själva verket aldrig vara helt skilda från varandra. Om vi koncentrerar oss på ett visst problem erinrar vi oss enbart fakta som har mer eller mindre klart samband med problemets avsikt, och det är detta mobiliserade material som skall organiseras.
Mobilisering och organisering är enbart två aspekter av samma komplicerade process som har ytterligare många aspekter.
4. En annan aspekt av att arbetet framskrider är att vår föreställning av problemet ändras. Utökad med allt det material som vi har kommit på och anpassat till problemet och arbetat in i det är vår föreställning av problemet mycket mera innehållsrik i slutet än den var i början. Eftersom vi strävar efter en bättre och mer adekvat föreställning av problemet än den vi ursprungligen hade, prövar vi olika ståndpunkter och betraktar problemet från olika sidor. Vi skulle knappast kunna göra några framsteg utan att Variera problemet.
5. När vi framskrider mot det slutliga målet ser vi mer och mer av det, och när vi kan se det bättre kan vi bedöma om vi kommit närmare. När vår undersökning av problemet framskrider kan vi allt klarare förutse vad som återstår av lösningen och hur den skall göras. Om vi löser ett matematiskt problem och har tur kanske vi kan förutse att en viss känd sats skulle kunna användas, att vi skulle kunna få hjälp av att använda ett visst tidigare löst problem eller att det kanske blir nödvändigt att gå tillbaka till innebörden av en viss fackterm. Vi kan inte förutse sådana saker med säkerhet, endast med en viss grad av sannolikhet. Säkerhet kommer vi att få när vi har kommit fram till den fullständiga lösningen, men innan dess måste vi ofta nöja oss med en mer eller mindre säker gissning. Utan reflexioner som ger enbart en möjlig och provisorisk utväg skulle vi aldrig kunna finna den lösning som är säker och slutgiltig. Vi behöver Heuristisk argumentation.
6. Vad innebär framsteg mot en lösning? ökande mobilisering och organisering av våra kunskaper, utveckling av vår föreställning av problemet, ökande förutseende om de steg som kommer att utgöra det slutliga argumentet. Vi kanske rör oss framåt stadigt med små omärkbara steg, men då och då avancerar vi plötsligt med stormsteg. Ett plötsligt skutt fram mot lösningen kan kallas en Ljus idé, en god idé, ett lyckligt infall, en snilleblixt. Vad är en ljus idé för något? En plötslig och viktig ändring av våra möjligheter, en plötslig förändring i vår föreställning av problemet, en just uppdykande säker vision av de åtgärder vi måste vidta för att komma fram till lösningen.
7. Den föregående framställningen ger en lämplig bakgrund till frågorna och uppmaningarna på vår lista.
Många av dessa frågor och uppmaningar syftar direkt att mobilisera de kunskaper som vi tidigare förvärvat: Har du sett detta förut? Har du sett samma problem i en något annorlunda form? Känner du till något närbesläktat problem? Känner du till någon sats som skulle kunna användas? Betrakta den obekanta! Försök finna ett känt problem med samma eller liknande obekanta storhet.
Det finns typiska situationer där vi anser oss ha insamlat det rätta materialet och där vi försöker få en bättre organisering av det som vi har mobiliserat: Här är ett närbesläktat problem som är löst förut. Skulle du kunna använda det? Skulle du kunna använda dess resultat? Eller dess metod? Skulle du kunna införa någon hjälpstorhet så att du kan använda det?
Det finns andra typiska situationer där vi anser oss ännu inte ha samlat tillräckligt material. Vi frågar vad som fattas: Använde du alla de givna uppgifterna? Använde du hela villkoret? Har du tagit hänsyn till alla nödvändiga begrepp som ingår i problemet?
En del frågor syftar direkt till variation av problemet: Skulle du kunna formulera om problemet? Skulle du kunna formulera om det ytterligare? Många frågor syftar till att variera problemet genom speciella metoder, som t.ex. att gå tillbaka till Definitionen, att använda Analogi, Generalisering, Specialisering, Uppdelning och rekombinering.
Andra frågor åter antyder ett försök att förutse arten av den lösning vi vill komma fram till: Är det möjligt att uppfylla villkoret? Är villkoret tillräckligt för att bestämma den obekanta? Eller är det otillräckligt? Eller överflödigt? Eller motsägelsefullt?
Frågorna och uppmaningarna på vår lista nämner inte direkt den ljusa idén, men alla handlar egentligen om den. När vi försöker förstå problemet förbereder vi oss för den. När vi gör en plan försöker vi framkalla den. När vi har framkallat den genomför vi den. När vi senare ser tillbaka på lösningens gång och resultat försöker vi att utnyttja den ännu bättre.|6|
Generalisering innebär att en utsaga som gäller ett visst objekt överflyttas till att gälla en viss mängd som innehåller objektet i fråga, eller att utsagan överflyttas från en begränsad mängd till en mer omfattande mängd som innehåller den begränsade.
1. Om vi genom någon tillfällighet råkar på summan 1 + 8 + 27 + 64 = 100, kanske vi lägger märke till att den kan uttryckas i den egendomliga formen 1³ + 2³ + 3³ + 4³ = 10². Nu kan man naturligtvis fråga sig: Inträffar det ofta att summan av successiva kuber, 1³ + 2³ + 3³ + … + n³, är en kvadrat? När vi ställer denna fråga generaliserar vi, och just denna gång har vi tur. Generaliseringen leder från en iakttagelse till en anmärkningsvärt allmän lag. Många resultat inom matematik, fysik och andra naturvetenskaper har härletts ur lyckosamma generaliseringar. Se Induktion och matematisk induktion.
2. Generaliseringar kan vara användbara vid problemlösning. Studera följande rymdgeometriska problem: "En rät linje och en reguljär oktaeder är kända till sina lägen. Sök det plan som går genom den givna linjen och som halverar volymen av oktaedern." Detta problem kanske verkar svårt, men i själva verket är redan obetydliga kunskaper om den reguljära oktaederns form tillräckliga för att antyda följande generellare problem: "En rät linje och en kropp med symmetricentrum är kända till sina lägen. Sök det plan som går genom den givna linjen och som halverar kroppens volym." Det plan som söks går naturligtvis genom kroppens symmetricentrum och det bestäms genom denna punkt och den givna linjen. Eftersom oktaedern har symmetricentrum är vårt ursprungliga problem också löst.
Läsaren kan inte undgå att lägga märke till att det andra problemet är mer allmänt än det första, men att det inte desto mindre är mycket lättare än det första. I själva verket var vår huvudsakliga prestation när vi löste det första problemet att komma på det andra problemet. När vi gjort det upptäckte vi den roll som symmetricentrum spelar. Vi frigjorde den egenskap hos oktaedern som är väsentlig för problemet i fråga, nämligen att den har ett symmetricentrum.
Det allmännare problemet kan vara lättare att lösa. Detta låter paradoxalt, men efter det här exemplet bör vi inte tycka det. Den huvudsakliga prestationen i lösningen av det speciella problemet låg i att upptäcka det allmänna problemet. Efter denna insats återstår bara en mindre del av arbetet. I vårt fall är alltså det allmänna problemets lösning bara en mindre del av det speciella problemets lösning. Se Uppfinnarparadoxen.
3. "Beräkna volymen av en stympad pyramid med kvadratisk bas. Höjden är 6 cm, de övre och undre kvadraternas sidor är 5 resp. 10 cm."
Om vi ersätter talen 6, 5, 10 med bokstäverna h, a, b generaliserar vi. Vi får ett allmännare problem än det ursprungliga, nämligen följande: "Beräkna volymen av en stympad pyramid med kvadratisk bas, vars höjd är h och vars kvadratiska sidor är a och b." En sådan generalisering kan vara mycket användbar. Genom att gå över från ett problem "i siffror" till ett annat "i bokstäver" öppnar vi vägen för nya metoder. Vi kan variera de givna uppgifterna och när vi gör det så kan vi kontrollera våra resultat i olika avseenden. Se Kan du kontrollera resultatet?, 2, Variera problemet, 4.
Granska gissningen. Din gissning kan vara riktig men det vore dumt att godta en vild gissning som en bevisad sanning — som förnöjsamma personer ofta gör. Din gissning kan vara felaktig. Men det vore lika dumt att helt bortse från en vild gissning — som petnoga personer ibland gör. Vissa gissningar bör studeras närmare mera allvarligt: De som dyker upp när vi har trängt in i och verkligen förstått det problem vi är intresserade av. Vanligtvis innehåller sådana gissningar åtminstone ett uns av sanning även om de naturligtvis mycket sällan visar hela sanningen. Men det finns en möjlighet att få fram hela sanningen om vi granskar en sådan gissning på ett lämpligt sätt.
Många gissningar kan visa sig vara felaktiga men ändå användbara om de leder till en bättre gissning.
Ingen idé är verkligt dålig, såvida vi inte är okritiska. Vad som är riktigt svagt är att inte ha någon idé alls.
1. Gör inte så. Här är en typisk historia om Karl Svensson. Herr Svensson arbetar på kontor. Han hade hoppats på en liten löneförhöjning men som så ofta sveks hans förhoppningar. Hans kollegers löner höjdes men inte hans. Svensson lät sig inte nöjas med detta. Han grubblade länge och till slut misstänkte han att det var direktör Jönssons fel att han inte fick det bättre.
Vi kan inte klandra Svensson för att han hyste en sådan misstanke. Det fanns i själva verket flera tecken som pekade på direktör Jönsson. Det verkliga misstaget Svensson begick var att han blev blind för alla tecken som pekade i motsatt riktning när han väl en gång hade fått misstanken. Han plågade sig själv tills han var fast övertygad om att direktör Jönsson var hans personliga fiende, och han uppförde sig så idiotiskt att han nästan lyckades med att göra direktören till en verklig fiende.
Felet med Svensson är att han uppför sig precis som de flesta av oss. Han ändrar aldrig mening i viktiga frågor, men han gör det ofta och helt plötsligt i bagatellfrågor. Men han ifrågasätter aldrig sina åsikter, varken i stora eller i små frågor — så länge han har dem. Han är aldrig osäker på dem eller ifrågasätter dem eller granskar dem kritiskt. Han skulle speciellt avsky kritisk granskning om han förstod vad som menades med det.
Låt oss medge att Svensson har rätt till en viss grad. Han har mycket att göra. Han har sina åligganden på kontoret och hemma. Han hinner inte med att tvivla eller granska. I bästa fall skulle han kunna granska bara några av sina åsikter och varför skulle han ifrågasätta någon av dem om han ändå inte har tid att undersöka dem? Men ändå, gör inte som Svensson. Låt inte din misstanke eller gissning eller förmodan stärkas tills den blir outrotlig utan att granska den. Under alla förhållanden gäller i teoretiska sammanhang att de bästa idéer torkar in om de accepteras okritiskt men bär frukt under kritisk prövning.
2. Ett matematiskt exempel. Sök den fyrhörning med given omkrets vars yta är störst.
Vad är det som söks? En fyrhörning.
Vad är det som är givet? Omkretsen av fyrhörningen.
Hur lyder villkoret? Den efterfrågade fyrhörningen skall ha större yta än någon annan fyrhörning med samma omkrets,
Detta problem liknar inte alls de vanliga problemen i elementär geometri och det är därför helt naturligt att man börjar gissa. Vilken fyrhörning har förmodligen den största ytan? Vilken skulle den enklaste gissningen vara? Kanske har vi hört att av alla figurer med samma omkrets så har cirkeln den största ytan. Vi kanske även anar något skäl för att detta påstående är riktigt. Men vilken fyrhörning liknar cirkeln mest? Vilken kommer närmast i symmetri?
Kvadraten är en ganska självklar gissning. Om vi tar denna gissning på allvar så måste vi inse vad den innebär. Vi får inte vara rädda för att formulera den: "Av alla fyrhörningar med en given omkrets har kvadraten den största ytan." Om vi beslutar oss för att undersöka detta påstående så ändras situationen. Ursprungligen hade vi ett "sökproblem". Efter att nu ha formulerat vår gissning har vi ett "bevisproblem". Vi måste bevisa eller vederlägga den formulerade satsen.
Om vi inte känner till något tidigare löst problem som liknar vårt kanske vi tycker att vår uppgift är ganska svår. Om du inte kan lösa det givna problemet, försök först lösa något liknande problem. Skulle du kunna lösa en del av problemet? Vi kanske kommer att tänka på att om kvadraten har en särställning bland fyrhörningar måste den av samma orsak också ha en särställning bland rektanglar. En del av vårt problem skulle vara löst om vi lyckades bevisa följande påstående: "Av alla rektanglar med given omkrets har kvadraten den största ytan."
Denna sats förefaller mera tillgänglig än den förra. Den är naturligtvis svagare. I vilket fall som helst bör vi tänka igenom vad den innebär. Vi får inte vara rädda för att formulera om den på ett utförligare sätt. Det är lämpligt att göra det med hjälp av algebrans språk.
Ytan av en rektangel med sidorna a och b är ab. En sida av kvadraten som har samma omkrets som rektangeln vi just nämnde har storleken (a + b)/2. Alltså är ytan av denna kvadrat lika med [(a + b)/2]². Den skall vara större än rektangelns yta och följaktligen måste gälla att [(a + b)/2]² > ab.
Är detta sant? Samma påstående kan skrivas i den ekvivalenta formen a² + 2ab + b² > 4ab. Detta är emellertid sant, ty det är ekvivalent med a² - 2ab + b² > 0 eller med (a - b)² > 0, och denna olikhet gäller med säkerhet såvida inte a = b, då den undersökta rektangeln är en kvadrat.
Vi har inte löst vårt problem än men vi har gjort ett visst framsteg enbart genom att granska vår tämligen självklara gissning.
3. Ett icke-matematiskt exempel. På ett visst ställe i ett korsord skall vi finna ett ord med 7 bokstäver och ledtråden lyder: "Do the walls again, back and forth."|7|
Vad är det som söks? Ett ord.
Vad är det som är givet? Ordets längd om 7 bokstäver.
Hur lyder villkoret? Det är formulerat i ledtråden och har någonting att göra med väggar, men det är mycket diffust.
Alltså måste vi granska ledtråden närmare. Vi kanske då lägger märke till den sista delen: "… again, back and forth." Skulle du kunna lösa en del av problemet? Här har vi en chans att gissa ordets början. Eftersom repetitionen är framhävd så starkt är det mycket möjligt att ordet börjar med "re". Detta är en ganska självklar gissning. Om vi är benägna att tro på den så bör vi undersöka vad den innebär. Det sökta ordet skulle se ut på följande sätt:
RE-----
Kan du kontrollera resultatet? Om ett annat ord korsar vårt i den första bokstaven har vi ett R som måste passa i det ordet. Det kan nu vara bra att gå över till detta andra ord och undersöka om R passar. Om vi lyckas få det att stämma eller om vi åtminstone inte finner något skäl som talar mot detta R, kan vi gå tillbaka till vårt ursprungliga ord. Vi frågar igen: Hur lyder villkoret? När vi undersöker ledtråden igen kan vi lägga märke till den allra sista delen av den: "… back and forth." Kan detta innebära att det ord vi letar efter kan läsas både framlänges och baklänges? Detta är en mindre självklar gissning (men det finns dock sådana fall, se Uppdelning och rekombinering, 8).
Låt oss i vilket fall som helst titta närmare på denna gissning och undersöka vad den innebär. Ordet skulle se ut på följande sätt:
RE---ER.
Dessutom skall då tredje bokstaven vara identisk med den femte. Den är sannolikt en konsonant och den mellersta är sannolikt en vokal.
Läsaren kan nu lätt gissa ordet själv. Om ingenting annat hjälper kan han försöka med den ena vokalen efter den andra för bokstaven i mitten.
Har du sett detta förut? Det är möjligt att vi tidigare har löst samma problem som vi ställs inför nu eller att vi har hört talas om det eller att vi har haft ett mycket likartat problem. Detta är möjligheter som vi inte får försumma att undersöka. Vi försöker komma ihåg vad som hände. Har du sett detta förut? Har du sett samma problem i en något annorlunda form? Även om svaret blir nej kan sådana frågor sätta fart på de användbara kunskaper vi har.
Frågan i rubriken används ofta i en mer allmän mening. För att komma fram till en lösning måste vi locka fram relevanta element ur vårt minne, vi måste väcka tillämpliga delar av slumrande kunskaper (Framsteg och prestation). Vi kan naturligtvis inte i förväg veta vilka delar av våra kunskaper som kan vara relevanta, men det finns vissa möjligheter som vi inte får underlåta att undersöka. Så kan t.ex. en viss detalj i det aktuella problemet, som vi vet spelade en roll i lösningen av ett annat problem, mycket väl spela samma roll igen. Om därför någon detalj i det föreliggande problemet synes oss betydelsefull, så försöker vi känna igen den sedan tidigare. Vad innebär den? Förefaller den bekant? Har du sett detta förut?